15

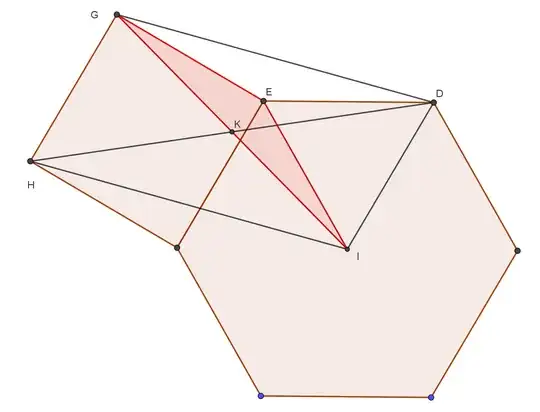
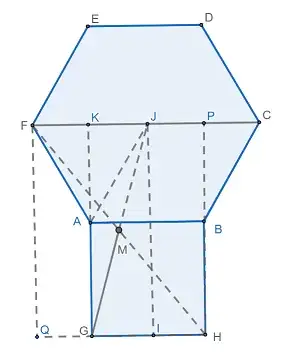
I want to find $\angle AGM=\theta$ in the following picture:
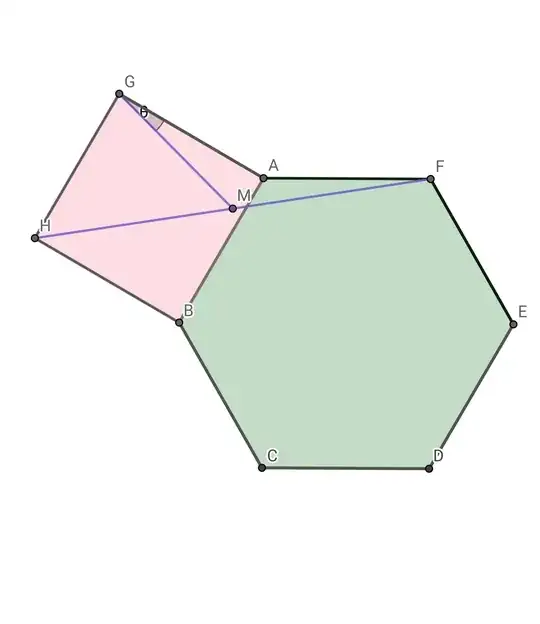Problem figure Here $ABCDEF$ and $BAGH$ are regular hexagon and square respectively and $M$ is the midpoint of $FH$.

I found a trigonometric solution. I'm providing key ideas of the solution:

Let $AB=1$. Now we can apply cosine rule on $\triangle AHF$ to find $HF$ and $HM$. Now in $\triangle MGH$, we can find $GM$ using cosine rule again and then find $\angle MGH$ by sine rule. This gives $\theta=15^{\circ}$. (I'm not providing the calculations as they are not nice and I did most of them with calculator.)

But I believe there are some beautiful synthetic solution to the but didn't find one. So, I need a synthetic solution to the problem.

nonuser
  • 91,557
Oshawott
  • 4,028

2 Answers2

24

Let $I$ be a center of hexagon. Then $HG = ID$ and they are parallel, so $IDGH$ is a paralelogram so $K$ is also the midpoint of $GI$, thus $G,K,I$ are collinear.

Since $GEI$ is isosceles triangle and $\angle GEI = 150^{\circ}$ we have $\theta = 15^{\circ}$.

enter image description here

nonuser
  • 91,557
  • Not doubting your answer, just requesting clarification: how did you get $\angle GEI = 150^{\circ}$? – blackbrandt Aug 26 '21 at 16:01
  • 5
    90+60 .................. @blackbrandt – nonuser Aug 26 '21 at 16:07
  • wow I actually feel dumb now :) i was totally overthinking that – blackbrandt Aug 26 '21 at 16:39
  • 3
    The statement that HG = ID is implicitly based on the fact that the length of a side of a regular hexagon is equal to the length from the center of the hexagon to any vertex, I believe. I think you should make that explicit; it took me only a few moments to realize that’s how you got that conclusion and convince myself that it was true, but it’s better for such things to be explicitly stated. Also, it’s a little confusing that you relabeled the points in question; your K is M in the question, your E is A, and your D is F. Makes things a little harder to follow. – KRyan Aug 26 '21 at 21:20
  • What are you talking? @KRyan That is what kids in elementary school learn/know. – nonuser Aug 27 '21 at 11:19
  • It is very plausible that I did learn it in elementary school, but it has been a long time since then and I don’t do a lot of hexagonal geometry in my daily life. – KRyan Aug 27 '21 at 12:09
16

Even without pure geometry, the work can be simplified. Also, see my edit at the end for a synthetic solution.

enter image description here

$\angle PBC = \angle AFQ = 30^\circ$

If side length is $a$, $PC = GQ = \frac{a}{2}$

So, $PF = HQ = \frac{3a}{2}$

Similarly, $PH = FQ = a + \frac{a \sqrt3}{2}$

Given $M$ is the midpoint of $FH$,

$MN = a - \frac{HQ}{2} = \frac{a}{4}$

$GN = \frac{FQ}{2} = \frac{a (2 + \sqrt3)}{4}$

$\tan \theta = \frac{1}{2 + \sqrt3} = 2 - \sqrt3 \implies \theta = 15^0$

Synthetic solution (using similar construct as above):

enter image description here

Given $M$ is the midpoint of $HF$, it is also the center of rectangle $HPFQ$ and hence of rectangle $GIJK$.

Also note $J$ is the center of the hexagon.

So, $\triangle FAJ$ is an equilateral triangle.

$\angle JAK = 30^\circ$.

In $\triangle GAJ$, $AG = AJ$

$\therefore \angle AGM = \angle AJM = 15^\circ$

Jakeup
  • 766
Math Lover
  • 52,200
  • 1
    (+1) This seems extremely close to a synthetic solution. In fact, also using synthetic methods, we can show that in the 15-75-90 triangle ($\triangle GMA$), the length of the altitude from the right angled vertex is 4 times the length of the hypotenuse (which also means that we should be able to show that $\angle GMA$ is a right angle). – krazy-8 Aug 25 '21 at 17:48
  • What is a synthetic solution? @dodoturkoz – Clemens Bartholdy Aug 26 '21 at 15:32
  • @Buraian that's a good point :) I would call it geometric construction that leads to the answer without using trigonometry / equations. Here is something I found - https://math.stackexchange.com/questions/669037/what-is-synthetic-geometry – Math Lover Aug 26 '21 at 15:47
  • @Buraian I agree with MathLover. Though, many times the distinction between synthetic and analytic methods is not very clear (as we can derive trigonometric results using synthetic geometry). – krazy-8 Aug 26 '21 at 16:12