I read that you must solve the two equations $$g(x,y,c)=0\\\frac{\partial g}{\partial c}=0$$ for $x$ and $y$ as a function of $c$, but how exactly do you go about doing this? The specific example I am trying to solve is where $$F(x,y,\alpha)= -t y \sin\alpha \tan{\alpha\over2} - t \sin\alpha \left(x - r \cos\alpha - t \sin\alpha \tan{\alpha\over2}\right)$$ and find the parametric equation for the envelope ($r$ and $t$ are constants). BTW, this is from this post if you are curious.
Asked
Active
Viewed 266 times
2
-
One possible simplification here is to make the half-angle tangent substitution $s=\tan(\alpha/2)$. Then $\cos\alpha = (1-s^2)/(1+s^2)$ and $\sin\alpha=2s/(1+s^2)$, so now we have $G(x,y,s):=F(x,y,2\tan^{-1} s)$ as some rational function of $x,y,s$. (It's still not exactly nice but it may be easier to compute with.) – Semiclassical Aug 21 '21 at 03:58
-
What is $t$? It does not appear as an argument to $F$. – robjohn Aug 21 '21 at 04:31
-
@robjohn $t$ and $r$ are constants. Sorry for not being very clear. – bravesheeptribe Aug 21 '21 at 04:35
1 Answers
2
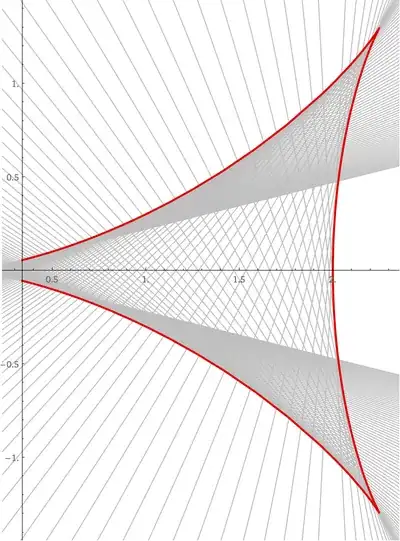
The curves given by $F(x,y,\alpha)=0$, are also given by $G(x,y,u)=0$ where $u=\tan\left(\frac\alpha2\right)$ and $$ \begin{align} G(x,y,u) &=\frac{F(x,y,\alpha)}{-t\sin(\alpha)}\tag{1a}\\ &=y\tan\left(\frac\alpha2\right)+\left(x-r\cos(\alpha)-t\sin(\alpha)\tan\left(\frac\alpha2\right)\right)\tag{1b}\\ &=yu+x-r\frac{1-u^2}{1+u^2}-t\frac{2u^2}{1+u^2}\tag{1c} \end{align} $$ Then, since $\frac{\partial}{\partial u}\frac{2u^2}{1+u^2}=\frac{4u}{\left(1+u^2\right)^2}$, $$ \frac{\partial}{\partial u}G(x,y,u)=y-(t-r)\frac{4u}{\left(1+u^2\right)^2}\tag{2} $$ Therefore, $\frac{\partial}{\partial u}G(x,y,u)=0$ when $$ y=(t-r)\frac{4u}{\left(1+u^2\right)^2}\tag3 $$ and then $G(x,y,u)=0$ when $$ x=t+(r-t)\frac{1+4u^2-u^4}{\left(1+u^2\right)^2}\tag4 $$
Example: $r=2,t=1$
robjohn
- 353,833