SU(5) Lie algebra: Derive the 10-dimensional matrix representation, from the given 5-dimensional fundamental matrix representation

Question

My question (Abstractly)

If we know how to write the matrix representation of the fundamental representation of SU(N), could we use them to derive the matrix representation of other representations of SU(N)? (adjoint, anti-symmetric, or symmetric, etc.)

For example, for SU(2), I asked a trial question here SU(2) Lie algebra: Derive the 3-dimensional adjoint matrix representation, from the given 2-dimensional fundamental matrix representation.

Now we aim to consider the SU(5) example.

---

We know the tensor product of 5-dimensional fundamental representation of SU(5) gives the 10-dimensional (anti-symmetric) representation and 15-dimensional (symmetric) representation of SU(5): $$ 5 \times 5 = 10_A + 15_S $$

---

It is easy to write down the 5-dimensional matrix representations of SU(5) with 24 Lie algebra rank-5 matrix generators as:

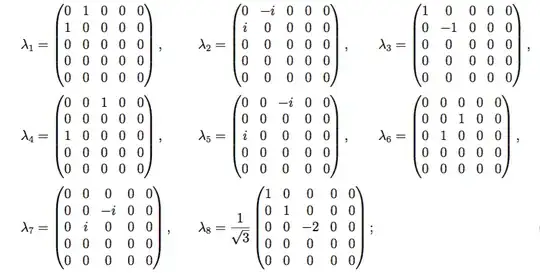
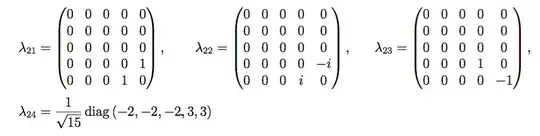
My question (Concretely)

is that based on the fact of $$ 5 \times 5 = 10_A + 15_S $$

How do we write down the 10-dimensional and 15-dimensional matrix representations of SU(5)?

• 10-dimensional matrix representations of SU(5) with 24 Lie algebra rank-10 matrix generators.

• 15-dimensional matrix representations of SU(5) with 24 Lie algebra rank-15 matrix generators.

Warning: Note that the $10_A$ is not just the rank-5 antisymmetric matrix as Lie algebra generators because that only gives 10 such matrices which generate the SO(5) instead of SU(5).

Answer 1

As Callum already pointed out, the required computations for a given basis are straight-forward, but quite tedious. Thus I propose to use a CAS to automize this. In Mathematica, this could look somewhat like this:

Recycling some code from 159030, we can generate some basis basissu of $\mathfrak{su}(5)$ (it is not the one given by OP, but one may replace basissu by any other custom basis):

n = 5;
a = 1/Sqrt[2] Flatten[
    Table[ 
      SparseArray[{{i, j} -> I, {j, i} -> I}, {n, n}], 
      {i, 1, n}, {j, i + 1, n}
      ], 
    1
    ];
b = 1/Sqrt[2] Flatten[
    Table[
      SparseArray[{{i, j} -> -1, {j, i} -> 1}, {n, n}], 
      {i, 1, n}, {j, i + 1, n}
      ], 
    1
    ];
c = DiagonalMatrix@*SparseArray /@ 
   Orthogonalize[
    Table[SparseArray[{{i} -> I, {i + 1} -> -I}, {n}], {i, 1, n - 1}]];
basissu = Join[a, b, c];

Now we generate an orthonormal bases for $\Lambda^2\mathbb{C}^5$:

e = IdentityMatrix[n];
innerprod[X_, Y_] := Tr[ConjugateTranspose[X].Y]
basis[CapitalLambda]2 = Orthogonalize[
   Flatten[
    Table[
     Normal[TensorWedge[e[[i]], e[[j]]]], {i, 1, n}, {j, i + 1, n}],
    1
    ],
   innerprod
   ];
basisS2 = Orthogonalize[
   Flatten[
    Table[
     Normal[
      TensorProduct[e[[i]], e[[j]]] + TensorProduct[e[[j]], e[[i]]]], {i, 1, n}, {j, i + 1, n}],
    1
    ],
   innerprod
   ];

(Curiously, there is a TensorWedge (corresponding to $\wedge$) in Mathematica, but no TensorDot (corresponding to $\odot$), so we had to roll out our own one.)

If I am not mistaken, the action of $\mathfrak{su}(5)$ on $\bigotimes^2 \mathbb{C}^5$ is given by the following.

action[A_] := X |-> Transpose[A].X + X.A

Next, we generate the Gram matrix (which is the identity matrix, just in case you want to use any non-orthonormal basis) and use it to represent the action of $A \in \mathfrak{su}(5)$ as matrix in terms of the chosen basis in $\Lambda^2 \mathbb{C}^5$.

invGramMatrix\[CapitalLambda]2 = 
  Inverse@
   Outer[innerprod, basis\[CapitalLambda]2, basis\[CapitalLambda]2, 1];
representationMatrix\[CapitalLambda]2[A_] := 
  Outer[innerprod, 
   invGramMatrix\[CapitalLambda]2 . basis\[CapitalLambda]2, 
   action[A] /@ basis\[CapitalLambda]2, 1];

Now we can map the function representationMatrix\[CapitalLambda]2 over the chosen basis of basissu

representationMatrix\[CapitalLambda]2 /@ basissu

For the symmetric tensors, the procedure is fully analogous:

basisS2 = Orthogonalize[
       Flatten[
        Table[
         Normal[
          TensorProduct[e[[i]], e[[j]]] + TensorProduct[e[[j]], e[[i]]]], {i, 1, n}, {j, i + 1, n}],
        1
        ],
       innerprod
       ];
invGramMatrixS2 = Inverse@Outer[innerprod, basisS2, basisS2, 1];
representationMatrixS2[A_] := Outer[innerprod, invGramMatrixS2.basisS2, action[A] /@ basisS2, 1];
representationMatrixS2 /@ basissu

Answer 2

If $V$, $W$ are representations of some Lie algebra $\mathfrak{g}$ then $V\otimes W$ is a representation with action given by:

$$ X(v\otimes w) = X(v) \otimes w + v \otimes X(w),$$

for each $X \in \mathfrak{g}$. You have the action of $\mathfrak{g} = \mathfrak{su}(5)$ given in some explicit basis $v_1,\dots,v_5$ of $V$ and then you are asking what the action looks like on $V \otimes V$. The simplest basis to pick would perhaps be $v_i \otimes v_j$ for each $i$ and $j$ and you could explicitly calculate what each of your generators does to each of these and you have a series of 25 by 25 matrices (blegh).

However, as you have noted the representation splits up into 2 irreducible representations so perhaps we can do better. What's going on here? Well the action of the Lie algebra commutes with the action of of the symmetric group (i.e. with swapping the order of $v_i \otimes v_j$) so $\bigwedge^2V$, the exterior square, and $\mathrm{S}^2V$, the symmetric square, have to be subrepresentations. These are respectively the spans of $v_i \wedge v_j$ and $v_i \odot v_j$ where we're thinking of these as:

$$v_i \wedge v_j = v_i \otimes v_j - v_j \otimes v_i$$ $$v_i \odot v_j = v_i \otimes v_j + v_j \otimes v_i$$

The exterior square has dimension 10 in this case and the symmetric square has dimension 15.

Now we have to be a little careful here as we are working with $\mathfrak{su}$ which is a real Lie algebra thought of as acting on a complex vector space.

For higher tensor powers we have the same ideas except there are more subrepresentations obtained by looking at the action of the symmetric group. We refer to this as Pleythism and this where Young tableaux and Clebsh-Gordon coefficients pop up to keep track of this.