In general, $\dfrac{df(g(x))}{dg(x)}$ means $\dfrac{df(u)}{du}\Biggr|_{\large{u=g(x)}}=f'(g(x)) \, .$ You want to consider the behaviour of the function $f$ when $g(x)$ is incremented by an infinitely small amount $dg(x)$ (notice that the fact that $g$ itself is a function is irrelevant here—you simply want to treat $g(x)$ as a variable like any other). So informally, we have
$$
\frac{df(g(x))}{dg(x)}=\frac{f(g(x)+dg(x))-f(g(x))}{dg(x)} \, .
$$
Nowadays, we tend to think in terms of limits instead of "infinitesimals", and so we would write
$$
\dfrac{df(g(x))}{dg(x)}=\lim_{h \to 0}\frac{f\left(g(x)+h\right)-f(g(x))}{h} \, .
$$
In your example,
$$
\frac{d(7^x)}{d(x^7)}=\frac{d\left(7^{\sqrt[7]{x^7}}\right)}{d(x^7)}=\frac{d\left(7^{\sqrt[7]{u}}\right)}{du}\Biggr|_{\large{u=x^7}}=\lim_{h \to 0}\frac{7^{\sqrt[7]{u+h}}-7^{\sqrt[7]{u}}}{h}\Biggr|_{\large{u=x^7}}=\lim_{h \to 0}\frac{7^{\sqrt[7]{x^7+h}}-7^{\sqrt[7]{x^7}}}{h} \, .
$$
This tells us that the quantities $x^7$ and $7^x$ are related by the function $u\mapsto 7^{\sqrt[7]{u}}$. Here is a plot of $7^{\sqrt[7]{u}}$ against $u$:
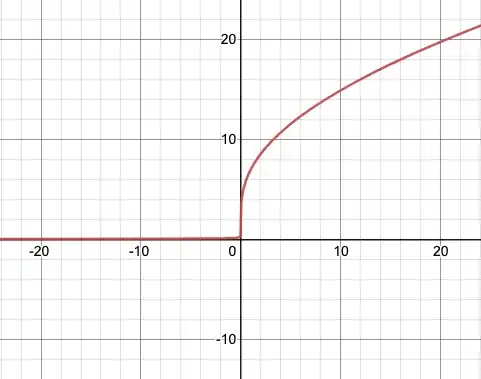
Using the chain rule multiple times tells us that
\begin{align}
\frac{d\left(7^{\sqrt[7]{u}}\right)}{du}\Biggr|_{\large{u=x^7}} &= \frac{1}{7} \cdot \log 7 \cdot 7^{\sqrt[7]{u}} \cdot u^{-6/7} \\[5pt]
&= \frac{7^x \cdot \log 7}{7x^6} \, .
\end{align}
Note that this result agrees with writing
$$
\frac{d(7^x)}{d(x^7)} = \frac{d(7^x)}{dx} \cdot \frac{dx}{d(x^7)} \, ,
$$
and using the inverse function theorem, which is probably the quickest way to arrive at the answer.
