I want to generalize the inverse transform sampling technique to a multidimensional setting. I have only seen this for the circle, as described in the motivation below, but I can't seem to find any good resources on the generalized problem.
The general setting I want to solve
Let $A = \prod_{i=1}^n (a_i,b_i) \subseteq \mathbb R^n$ be a rectangular cuboid and let
$$ \Phi \colon A \to M $$
be a diffeomorphism onto a bounded set $M \subseteq \mathbb R^n$. I want to find a measurable function
$$ \Psi \colon ((0,1)^n, \mathcal B_{(0,1)^n}, \lambda_{(0,1)^n}) \to (A,\mathcal B_A)$$
such that the random variable
$$ \Phi \circ \Psi \colon ((0,1)^n, \mathcal B_{(0,1)^n},\lambda_{(0,1)^n}) \to (M, \mathcal B_M)$$
has uniform distribution with respect to $\lambda_M$.
Note that for a Borel-measurable set $S \subseteq \mathbb R^n$, we denote by $\mathcal B_S$ the Borel sigma-algebra on $S$, and by $\lambda_S$ the Borel-measure or Lebesgue-measure on $S$.
[Please correct me in the following if you find any errors, but it seems to be true.]
With the identity $f = \lvert \operatorname{Det}D\Phi \rvert / \int d\lambda_M$, the question I ask above is the same as asking the following.
Let $f \colon A \to [0,\infty)$ be a measurable function such that $\int f d\lambda_A = 1$. Define the measure $\mu_f : = \int f d\lambda_A$ on $(A, \mathcal B_A)$. We want to find a measurable function
$$\Psi \colon ((0,1)^n, \mathcal B_{(0,1)^n}) \to (A, \mathcal B_A) \;,$$
such that the resulting random variable $$\Psi \colon ((0,1)^n, \mathcal B_{(0,1)^n}, \lambda_{(0,1)^n}) \to (A, \mathcal B_A) \;,$$ has uniform distribution with respect to $\mu_f$. This is the same as finding such a $\Psi$ such that $\lambda_{(0,1)^n} \circ \Psi^{-1} = \mu_f$.
For $n=1$, this is exactly inverse transform sampling (as shown below).
Motivation
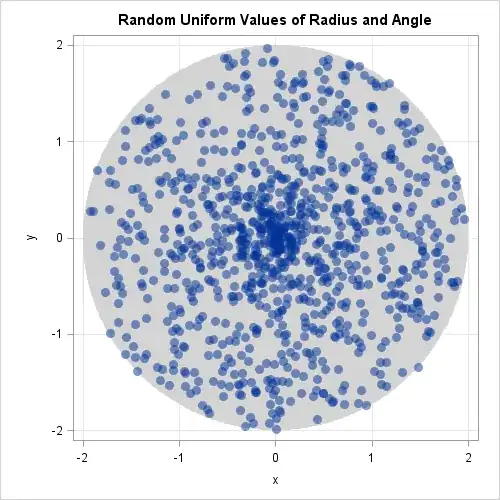
If we want to generate points in a circle $D^2$ randomly but uniformly on a computer, it is a bit tricky. We cannot easily say "create points uniformly on a circle", as most programming languages only provide uniformly generated random points on an interval. But we have the polar coordinate transformation
$$ \Phi \colon (0,R) \times (0,2 \pi) \to D^2 \;,$$
so we can randomly choose points on those two intervals, right? Wrong! What we would get is the following.
This polar coordinate transformation "stretches and squashes" space non uniformly, making the points denser for smaller radii and less dense for larger radii. So we need to somehow transform the randomly generated points before we transform them to the disc in the end.
The answer is to randomly generate points uniformly on $(0,1)^2$, and then apply the function
$$\Psi \colon (0,1)^2 \to (0,R) \times (0,2\pi)\;, \; (r,\theta) \mapsto (R\sqrt{r}, 2\pi\theta) \;,$$
and only then apply the polar coordinate transformation $\Phi$, after which we get the desired result.
I want to generalize this.
My problem
I totally understand the intuition behind it. There are many resources that give a good explanation for this specific example, but I see no satisfying proof of the result in a way that I can generalize it.
- https://blogs.sas.com/content/iml/2016/03/30/generate-uniform-2d-ball.html (which is where I got the images)
- https://stats.stackexchange.com/questions/481543/generating-random-points-uniformly-on-a-disk
- https://stackoverflow.com/questions/5837572/generate-a-random-point-within-a-circle-uniformly/50746409#50746409
- https://quantinterview.github.io/Random-Point-Circle/
I struggle to generalize this problem.
My try to solve it
The inverse transform sampling method allows the following. (Note: All sigma algebras are implied to be the borel/lebesgue sigma algebra.)
Let $f \colon (a,b) \to [0,\infty)$ be a density function (i.e. it has to be measurable and $\int_{(a,b)} f d\lambda = 1$). Define the probability density measure $\mu \colon = (E \mapsto \int 1_E f d\lambda_{(a,b)})$.
We can then find a measurable function $\Psi \colon (0,1) \to (a,b)$, such that $\lambda_{(0,1)} \circ \Psi^{-1} = \mu$, namely $\Psi = F^{-1}$ for $F = (x \mapsto \int 1_{(a,x)} f d\lambda_{(a,b)})$, the cumulative distribution function.
I tried to do multiple fubinis where I integrate every coordinate fully except for one, after which I have the one dimensional version of this problem. But then it didn't seem to all tie up nicely in the end. That solution to the problem, if it worked, also would mean that every coordinate gets transformed independently to $A$, which doesn't feel right. Or does that work?