3

I was curious about ways to sample perfectly dispersed points on the surface of the sphere. This question had some interesting info: Is the Fibonacci lattice the very best way to evenly distribute N points on a sphere? So far it seems that it is the best?

https://mathworld.wolfram.com/SphericalCode.html

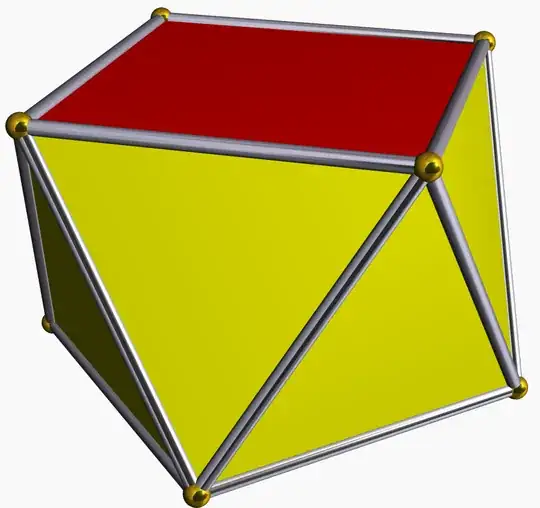
For two points, the points should be at opposite ends of a diameter. For four points, they should be placed at the polyhedron vertices of an inscribed regular tetrahedron. There is no unique best solution for five points since the distance cannot be reduced below that for six points. For six points, they should be placed at the polyhedron vertices of an inscribed regular octahedron. For seven points, the best solution is four equilateral spherical triangles with angles of 80 degrees. For eight points, the best dispersal is NOT the polyhedron vertices of the inscribed cube, but of a square antiprism with equal polyhedron edges. The solution for nine points is eight equilateral spherical triangles with angles of $\cos^{-1}(1/4)$. For $12$ points, the solution is an inscribed regular icosahedron.

I can't comprehend how a platonic solid does not perfectly uniformly sample the sphere surface. Is an intuitive explanation of this fact possible?

PNT
  • 4,295
berala
  • 153
  • 2
    The vertices of the cube do uniformly sample the sphere, they are just not the "best" way to do it in every measure. Sometimes too much symmetry prevents you from attaining the optimum. – M. Winter May 26 '21 at 13:52

2 Answers2

4

I think the intuition here is 'triangles are better than squares'. Squares aren't always avoidable, but a triangular configuration of vertices is more 'rigid' than a square one; it's easier to make small perturbations of the verts of a square that increase all the distances. In this case, by twisting the upper face $45^\circ$ you're increasing the minimum distance between verts on the upper face and those on the lower face, which means that you can in turn 'compress' those two faces closer to each other (i.e., bring them closer towards the equator of the sphere) to make the side lengths of the faces bigger while still maintaining inscribability. Similarly, while the icosahedron is optimal for 12 points because of the triangular facets, I would be very surprised if the best 20-point configuration were dodecahedral.

Steven Stadnicki
  • 53,147
  • In fact, triangles are enough better than squares that I'm surprised the optimal configuration isn't the north and south poles plus a triangular antiprism spaced to maximize the minimum distances... – Steven Stadnicki May 25 '21 at 17:05
  • 1
    Your description is actually a cube. The north and south poles squeeze the antiprism in such a way that you create square faces around the poles. You get a more optimal configuration if you allow the bases of the triangular antiprism to twist past each other. – Oscar Lanzi Aug 12 '22 at 23:07
  • 1
    @OscarLanzi I was wondering if I was going to get called out on that. :-) I noticed that sometime after I posted this but never got around to correcting it... – Steven Stadnicki Aug 13 '22 at 00:32
  • Try your method with 12 points, thus the two poles plus a pentagonal antiprism. What (true optimum) do you get then? – Oscar Lanzi Aug 13 '22 at 00:39
2

What I found to be most explanatory was the fact that each vertex of a cube (sub optimal) is equidistant to 3 other vertices whereas each vertex of a square antiprism is equidistant to 4 other vertices.

Of course, square antiprism is not as symmetric as a cube. However, a square antiprism does have perfect vertex symmetry (all 8 vertices are the same). I guess the fact that there are two kinds of facets and two kinds of edges is not relevant (or perhaps even slightly beneficial) to the sphere sampling because we are interested in the location of the vertices, which are indeed symmetric.

enter image description here

enter image description here

berala
  • 153
  • I checked this answer for eight points against the computer-generated results given at https://stackoverflow.com/questions/21977328/uniform-distribution-of-points-on-the-surface-of-a-sphere. The computer results for eight points forces one of them at (1,0,0), so the geometry is hard to tell from the coordinates, but by rendering point-to-point distances I find they conform with the square antiprism. +1. – Oscar Lanzi Aug 12 '22 at 23:43