6

Essentially, linearly separable points are just those corners that can be cut off with just one slice as marked out by a hyperplane.

E.g. for a cube, the following 4 points (red) are not linearly separable - no single cut by a plane (tilted at whatever angle) across the cube can slice off exactly these 4 points:

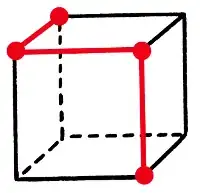
enter image description here

So this begs the question: given $n$ points on an $m$-dimensional hypercube, how can I tell if these $n$ points are linearly separable?

Rodrigo de Azevedo
  • 23,223
mchen
  • 595
  • @AsalBeagDubh - thanks, sounds like that might be what I want, but what is $p_i - p_0$? – mchen Jun 05 '13 at 15:40
  • Sorry, I deleted my comment because I think I misread the question. $p_i-p_0$ just means the vector pointing from the point $p_0$ to the point $p_i$. –  Jun 05 '13 at 17:03
  • related http://math.stackexchange.com/questions/18056/how-many-presentable-boolean-functions-with-n-attributes-are-linear-separable – leonbloy Jun 09 '13 at 18:34

1 Answers1

3

This is a crucial problem in machine learning, much studied since the 60's and there is no easy characterisation or criterion - nor even efficient algorithms. See eg this and this, , and references, or google for "Threshold Logic".

leonbloy
  • 66,202