what do holomorphic functions 'look like'? Please provide references.

Question

Question 1: What do holomorphic functions 'look like'? Not really sure what is meant by this, but I heard this was asked this in an interview for graduate school admissions.

What I have in mind is that

A. holomorphic functions are conformal, infinitely complex differentiable or something (not sure of the precise wording, but i guess it's like 'complex smooth'), equivalent to complex analytic (therefore we can just drop the qualifier 'complex') and have harmonic real and imaginary parts (i didn't learn in elementary complex analysis, but in miranda's book 'harmonic' is defined precisely as this. in elementary complex analysis, i learned holomorphic implies harmonic parts). Not really sure how to graph any of these, but the conformal thing is on wiki.
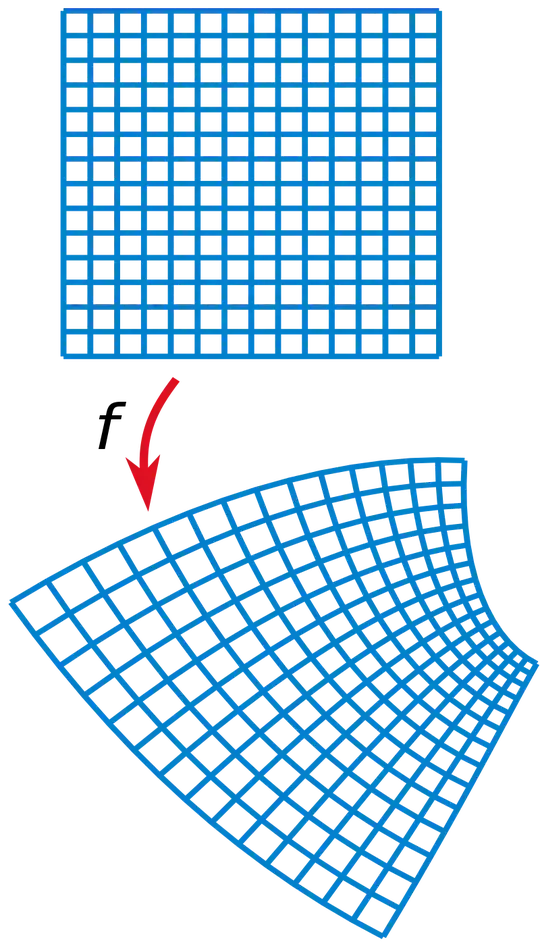
Here's the picture:
B. when you're asked what continuous functions $f: \mathbb R \to \mathbb R$ 'look like', intuitively/heuristically, you can draw a part of it on a paper without lifting your writing utensil from the paper. so you probably just do something that looks like sin/cos or a polynomial. (i remember in calc 1, the 1st continuous functions we're introduced to are these smooth functions sin/cos and polynomials.) I think this is kind of what the question means.
C. from the very definition itself, i just think to draw some circles like $g: \mathbb C \to \mathbb C$ holomorphic at $z=w$ means complex differentiable in some disc/disk around $z=w$. but i guess i'm just making drawings on its domain rather drawing the function itself.

Question 2: what books answer this?

Question 3: In relation to (B) above I actually find this question kind of weird. I mean does it make sense to ask what differentiable real functions $f: \mathbb R \to \mathbb R$ 'look like' ? twice differentiable functions $f: \mathbb R \to \mathbb R$ 'look like'? thrice? smooth functions $f: \mathbb R \to \mathbb R$? real-analytic functions?

Question 4: What do poles look like? what do poles 'look like'? Please provide references.

Update: Based on the comments below, this version of the Maximum modulus principle seems to be relevant:

Let $D \subseteq \mathbb C$ be bounded, non-empty and open. Suppose $f: \overline D \to \mathbb C$ is continuous on $\overline D$ and holomorphic on $D$. Then $|f|$ attains a maximum at some point in boundary of $D$ (i guess topological boundary, and i guess equal to $\overline D \setminus D$).

The comments Severin Schraven ( 2021Mar15 ) include:

It makes quite a lot of sense to ask this question in my opinion. The point is that holomorphic functions have a lot of structure and force them to have certain features. (...) The maximum principle is a very strong property. General continuous functions can be extremely wild!

A comment of Moishe Kohan ( 2021Apr19 ) :

Strictly speaking, the question is meaningless unless the meaning of "looks like" is specified. For this reason, no self-respecting textbook will discuss this, nor an interviewer at a grad school interview. They may ask: "What local properties of holomorphic functions do you know?" This would be a reasonable "long list" question.

God bless you, Moishe Kohan.

It makes quite a lot of sense to ask this question in my opinion. The point is that holomorphic functions have a lot of structure and force them to have certain features. The key here is the maximum principle if you are familiar with that. Try to draw a function that satisfies this, then you will understand :) — Severin Schraven, Mar 15 '21 at 11:10
@SeverinSchraven ah so you mean this is specific to holomorphic in that maybe it doesn't make quite sense to ask what continuous, differentiable, ..., real-analytic, etc functions look like, but we might ask this for holomorphic? — BCLC, Mar 15 '21 at 11:18
Exactly. The maximum principle is a very strong property. General continuous functions can be extremely wild! — Severin Schraven, Mar 15 '21 at 11:24
@SeverinSchraven right thanks. do you mean this 'related statement' of the maximum modulus principle? So far the maximum principles I'm seeing in my books on riemann surfaces and elementary complex analysis are either for harmonic functions $u: \mathbb R^2 \to \mathbb R$ or just conditions for a holomorphic function on a riemann surface to be constant (much like the original 'maximum modulus principle' in the aforementioned wiki link) — BCLC, Mar 15 '21 at 11:35
holomorphic functions look locally like powers - if $f$ holomorphic in some domain $U$ then for each $w \in U$ there is a small disc around $w$ contained in $U$ and unique $n \ge 1$ for which the function "looks like" $f(z)=a+b(z-w)^n$ with $b \ne 0$ and $a,b$ depending on $w$; this seemingly innoucous statement is actually very powerful and gives among other things, the maximum modulus principle, the discreteness of zeroes, results about conformality etc; — Conrad, Mar 15 '21 at 13:29
@Conrad (part1) thanks 1 - oh i recall reading this in Miranda's book. i believe this applies to riemann surfaces that aren't necessarily compact. in this case we could actually do $f(z)=z^n$, i think. do you know of any... — BCLC, Mar 17 '21 at 04:18
Conrad (part2) ...elementary complex analysis book (i guess something without surfaces, geometry, etc) that has this? 2 - so wait is this perhaps stronger than the description of @SeverinSchraven ? — BCLC, Mar 17 '21 at 04:18
@Conrad btw is there a way that real differentiable functions or real-analytic or real smooth or whatever 'look like' powers, but perhaps in a less powerful way than holomorphic functions? I recall there were ways to approximate $e^x$ as like $x+$ something, but of course there's no unique $n$ here or something. actually i recall further you can kinda approximate a lot of real functions (at least smooth i guess, but i think not necessarily real-analytic) without powers and then use taylor to compute the error. — BCLC, Mar 18 '21 at 12:32
Real analytic functions can always locally be extended to a complex analytic function on a small disc around any interior point in the domain; the famous example of $e^{-1/x^2}$ which has a zero of infinite order at the origin shows that it is hopeless in the smooth case to think like that — Conrad, Mar 18 '21 at 12:56
@Conrad thanks. wait why zero of infinite order rather than 'pole of infinite order' (which i understand is a way to think of essential singularity)? — BCLC, Mar 21 '21 at 08:27
The above (defined as zero at zero) is smooth $C^{\infty}$ as a real function and has a zero of infinite order; of course as a complex function there is an essential singularity there and the image of any small punctured disc is the punctured plane; this example shows why for real smooth functions is hopeless to get local models like in the complex case — Conrad, Mar 21 '21 at 13:15
Strictly speaking, the question is meaningless unless the meaning of "looks like" is specified. For this reason, no self-respecting textbook will discuss this, nor an interviewer at a grad school interview. They may ask: "What local properties of holomorphic functions do you know?" This would be a reasonable "long list" question. — Moishe Kohan, Apr 19 '21 at 16:57
@MoisheKohan God bless you. I am adding your comment to the OP. — BCLC, Oct 04 '21 at 13:11
@MoisheKohan 1 - what do you think of Conrad's answer re powers? it could be like holomorphic functions look like power $f(z)=a+b(z-w)^n$ 2 - re 'no self-respecting textbook will discuss this' what about Ahlfors or Needham's Visual Complex Analysis 3- what about the link of Andrew D. Hwang? — BCLC, Oct 27 '21 at 20:44
thanks @AndrewD.Hwang ! btw, what do poles look like? looks like your link about the 'Complex Polynomial Mappings' is related to my idea about the complex plot of $\frac 1 z$ — BCLC, Oct 27 '21 at 21:37
I can only repeat my objection to usage of the undefined notion "looks like". — Moishe Kohan, Oct 29 '21 at 00:36
@MoisheKohan thanks. had to change link. is there anyway poles are like vertical asymptotes? — BCLC, Feb 14 '25 at 06:24
@Conrad wait i think i remember. 1 way to view holomorphic functions $F$ is their local normal form at some point $p$ where they're locally polynomials actually monomials with unique power $n$ called the multiplicity of $f$ at $p$? ah so essentially search any complex analysis book for multiplicity or order $m$ of a point $p$ that's a zero or a pole or something and then it will tell you the integer $m$ where $f$ is like a monomial with power $m$? — BCLC, Feb 14 '25 at 06:43
@MoisheKohan wait i think i remember. 1 way to view holomorphic functions $F$ is their local normal form at some point $p$ where they're locally polynomials actually monomials with unique power $n$ called the multiplicity of $f$ at $p$? ah so essentially search any complex analysis book for multiplicity or order $m$ of a point $p$ that's a zero or a pole or something and then it will tell you the integer $m$ where $f$ is like a monomial with power $m$? — BCLC, Feb 14 '25 at 06:43
Yes correct - holomorphic functions are locally a monomial (and if they are meromorphic they are like a negative power monomial at the poles) — Conrad, Feb 14 '25 at 13:35
@Conrad ah yeah so it's like ... continuous functions locally you can draw without lifting from paper, holomorphic are locally monomial, manifolds are locally euclidean (plus other assumptions), immersions are local embeddings (and conversely), etc? and maybe the continuous function thing can have a similar description in terms of open sets... oh right yeah epsilon-delta but now more generally in open sets — BCLC, Feb 15 '25 at 23:55
@MoisheKohan can 'looks like' refer to local descriptions? eg continuous functions locally you can draw without lifting from paper, holomorphic are locally monomial, manifolds are locally euclidean (plus other assumptions), immersions are local embeddings (and conversely), etc? and maybe the continuous function thing can have a similar description in terms of open sets... oh right yeah epsilon-delta but now more generally in open sets — BCLC, Feb 15 '25 at 23:56
This is too vague. One can say that locally every holomorphic function is semiconjugate to the map $z\mapsto z^n$ (near $0$) for some $n\ge 0$. But this was already discussed on this site in the past. — Moishe Kohan, Feb 16 '25 at 00:09

score 3 · Accepted Answer · answered Apr 23 '21 at 02:52

Setup

A holomorphic function $f$ may be constant (and every constant function is holomorphic), in which case its effect on the input plane would be to send it all to a single point, and its graph in four real dimensions would look like a translation of the input plane. Constant functions are exceptional in many ways, so for the rest of this discussion, suppose that that $f$ is not constant.

Local

One way to “look” at a function is to consider “local” properties that can be seen when you look at the effect on a small neighborhood of a point in the domain.

Complex

The derivative $f'$ exists and is also holomorphic, and is not constantly zero since $f$ is not constant, so $f'$ has countably many isolated zeros. And the order of each zero is finite.

For every point $a$ that is not a zero of $f'$, there is a neighborhood of $a$ on which $f$ is conformal (preserving angles including their orientation/sense). And sufficiently close to $a$, $f$ is well-approximated by the action of complex multiplication by $f'(a)$, which has the effect of scaling by $\left|f'(a)\right|$ and rotating by $\mathrm{Arg}\left(f'(a)\right)$ (as a consequence, a small enough circle centered at $a$ is sent to a good approximation of a circle centered at $f(a)$).

For every point $b$ that is a zero of $f'$, since the order of the zero is finite, $f$ acts near $b$ like $f(z)\approx f(b)+c(z-b)^{n+1}$ for some positive integer $n$, so that $f$ has the effect of multiplying angles at $b$ by a factor of $n+1$ (by DeMoivre's Theorem, say). A small enough circle centered at $b$ is sent to a curve that approximates going around $f(b)$ in a circle $n+1$ times.

Components

If we instead want to understand what $f$ looks like by examining its components individually, we note that the components of $f$ are harmonic. This means that $\Delta u=\nabla\cdot\nabla u=0$, so that, by the flux form of Green's theorem, the flux integral of $\nabla u$ around a small circle is approximately zero. But this, combined with the continuity of $\nabla u$ coming from the infinite differentiability of $f$ (say) has the consequence that the average displacement of $u$ around a small circle is approximately zero, by the following calculation (see this Khan academy video for some visual intuition): $${\displaystyle \lim_{r\to0}}\dfrac{1}{2\pi r}\oint u\left(x+r\cos t,y+r\sin t\right)-u(x,y)\,\mathrm{d}t$$ $$=\dfrac{1}{2\pi}{\displaystyle \lim_{r\to0}}\oint\dfrac{u\left(x+r\cos t,y+r\sin t\right)-u(x,y)}{r}\,\mathrm{d}t$$

$$=\dfrac{1}{2\pi}{\displaystyle \lim_{r\to0}}\oint\nabla u\left(x+r\cos t,y+r\sin t\right)\cdot\left\langle \cos t,\sin t\right\rangle \,\mathrm{d}t$$

$$=\dfrac{1}{2\pi}{\displaystyle \lim_{r\to0}}\oint\nabla u\left(x+r\cos t,y+r\sin t\right)\cdot\mathrm{d}\hat{\mathbf{n}}$$

$$=0\text{ since }\Delta u=0$$

This is not a trivial claim because if $f$ is not constant, then either component must not be constant either, by the Cauchy-Riemann Equations.

Globally

If we look more broadly than a tiny neighborhood of a point, we would find that the maximum modulus principle (and the related maximum principle for the harmonic components) limits the way $f$ and $u$ can look even further.

And if $f$ is entire, then Picard's little theorem tells us that all values except perhaps one are attained somewhere.

References

Most of this is in many standard texts on Complex Analysis, like Ahlfors. I can edit in theorem/page references if desired.

Totally forgot to log in. Thank God for auto award. thank you very very much Mark S. btw do you agree with Moishe Kohan's comment (that i edited into the OP) ? — BCLC, Oct 04 '21 at 13:13
@John Smith Kyon, I agree that the phrase "looks like" is quite vague (see the different points of view in my answer), but wouldn't say that I agree that textbooks wouldn't discuss this. In some sense, Needham's Visual Complex Analysis is all about what complex functions "look like" from various perspectives. It would be a very bad exam question, but for an interview question, it sounds intentionally open-ended and fine to me. — Mark S., Oct 04 '21 at 13:29
Mark S., what do you think of the link of Andrew D. Hwang? i mean is it related to anything you said? — BCLC, Oct 27 '21 at 20:44
2- i learned continuous 'look like', intuitively/heuristically, you can draw w/o lifting pen from paper... so you probably just do something that looks like sin/cos or a polynomial. (i remember in calc 1, the 1st continuous functions we're introduced to are these smooth functions sin/cos and polynomials.) here indeed you're analogous answer is like 'f acts near b like', 'f′ has countably many isolated zeros', 'And sufficiently close to a , f is well-approximated by the action of complex multiplication' ? — BCLC, Feb 14 '25 at 00:36
3 - may you please illustrate this 'A small enough circle centered at b is sent to a curve that approximates going around f(b) in a circle n+1 times.' ? — BCLC, Feb 14 '25 at 06:25
4 - wait i think i remember. 1 way to view holomorphic functions $F$ is their local normal form at some point $p$ where they're locally polynomials actually monomials with unique power $n$ called the multiplicity of $f$ at $p$? ah so essentially search any complex analysis book for multiplicity or order $m$ of a point $p$ that's a zero or a pole or something and then it will tell you the integer $m$ where $f$ is like a monomial with power $m$? — BCLC, Feb 14 '25 at 06:42