2

Assume that $ΔABC$ is an isosceles triangle with base of length 3, and sides of length 4.

The main question is:

What is the area of the largest equilateral triangle that can be inscribed in $ΔABC$?

And, if we find a value, how can we prove that it's the biggest possible value and there exists no other equilateral triangle inscribed in $ΔABC$ with a larger area?

(I know that for an equilateral triangle, having the largest area is the same as having the largest side length, but the main question is to find the numerical value of the largest area)

What I have done so far:

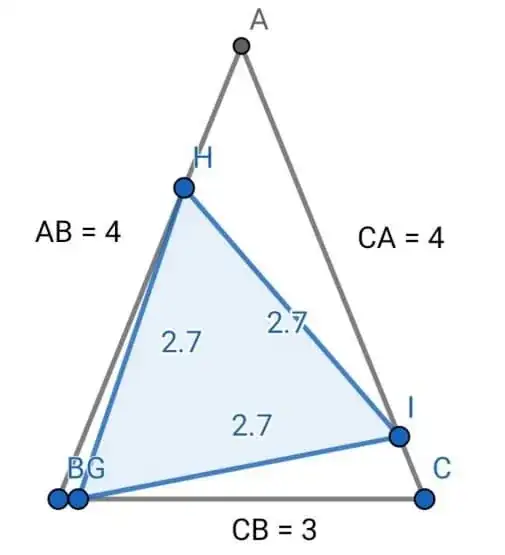
  1. I tried to play around with shapes in GeoGebra, in hope of finding an idea to solve the problem (something like using rotations, etc.). but it wasn't that helpful. geogebra_playaround

A problem is that the values on the image are not accurate, so I need a mathematical proof rather than only drawings, to show that a value is the largest one.

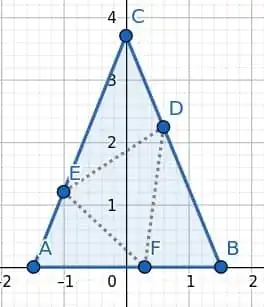
  1. I tried to draw the isosceles triangle on a xy-plane:

xyplane

(The height of the triangle is $\frac{\sqrt{55}}{2} \approx 3.7$ using the Pythagorean theorem)

First, I calculated line equation for each edge, then I chose 3 arbitrary points $P_1$ and $P_2$ on the sides (shown with $E$ and $D$ on the image) and $P_3$ on the base (point $F$ in the figure) with coordinates $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ respectively. Then I tried to rewrite $y_1$ and $y_2$ using $x$'s and the line equations. Then I used the formula for Euclidean distance and inserted $x$'s and $y$'s inside the formula and put each pair of distances in equation (since they are side lengths of an equilateral triangle). Eventually, I started to solve the equations and continue that way to establish a relation between the coordinates, however, it wasn't successful, or at least I wasn't able to derive any result.

Thanks in advance!

M. Bagheri
  • 57
  • 1
    You may get some insight from here but in your example I think it should be equilateral triangle with side length $3$. https://math.stackexchange.com/questions/2379188/finding-the-largest-equilateral-triangle-inside-a-given-triangle#:~:text=If%20only%20one%20angle%20in,in%20the%20OP's%20first%20figure. – Math Lover Mar 08 '21 at 14:05
  • Thanks for your response @MathLover . I have tried an equilateral triangle with side length 3, I can put two of the vertices on the edges of isosceles, but the third vertex always remains out of the main triangle. (I'm still unable to prove what I say) – M. Bagheri Mar 08 '21 at 14:32
  • That should not be the case given both angles at the base are equal and greater than $60^0$. The third vertex will be inside the given triangle. – Math Lover Mar 08 '21 at 14:39
  • 1
    Yes, but if the equilateral triangle lie on the base, it's no longer inscribed in the main triangle. (Its vertices should be on the edges of the main triangle) – M. Bagheri Mar 08 '21 at 14:46
  • Yes in that case you are right. Side length $3$ is not possible. – Math Lover Mar 08 '21 at 14:48
  • It is fairly clear in your example (given you want all vertices on the boundary) that it is largest when G=B. This is because if you rotate the inner triangle clockwise, all its vertices would move to the inside, after which you could enlarge it till it touches the sides again. This process only stops when G hits the corner B. In general you will have two vertices on one side of the outer triangle and at least one of the vertices coinciding with the outer triangle vertex with the largest angle. The case of obtuse outer triangles with angle >120 should be proved separately. – Jaap Scherphuis Mar 08 '21 at 15:46

1 Answers1

1

If we set (see your first figure) $BG=x$, $CG=3-x$, $\angle ABC=\angle ACB=\alpha$, $\angle CGI=\theta$, $GI=IH=HG=l$, then by the sine rule applied to triangles $GCI$ and $BGH$ we obtain: $$ {l\over\sin\alpha}={3-x\over\sin(\alpha+\theta)}={x\over\sin(60°+\theta-\alpha)}. $$ We can solve for $x$ to find: $$ x={3\over2}\left(1-{\tan(\alpha-30°)\over\tan(30°+\theta)} \right). $$ Substituting that into the expression for $l$ and differentiating one gets $$ {dl\over d\theta}=-{3\over2}{\sin\alpha\over\sin(60°+\theta-\alpha)} \big(1-\tan(\alpha-30°)\big)\cot(30°+\theta). $$ This vanishes only for $\theta=60°$, but that is a minimum (as one can deduce from the sign of $dl/d\theta$). Hence maxima are attained at the boundary values of $\theta$, which are the values for which $x=0$ or $x=3$, that is $\theta=\alpha-60°$ and $\theta=180°-\alpha$.

This gives as a maximum for $l$: $$ l_\max={3\sin\alpha\over\sin(2\alpha-60°)}. $$

Intelligenti pauca
  • 55,765