1

I do not have a background in mathematics. I am a developer attempting to process point cloud data, but I believe this to be the correct place to post for this type of problem.

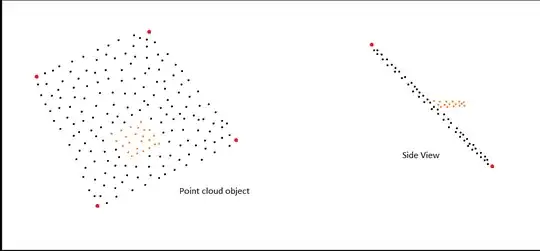
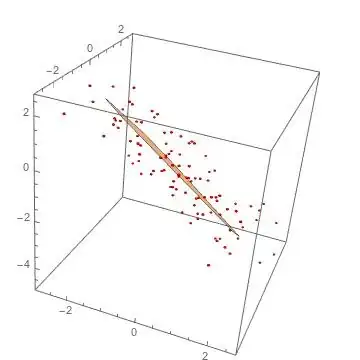
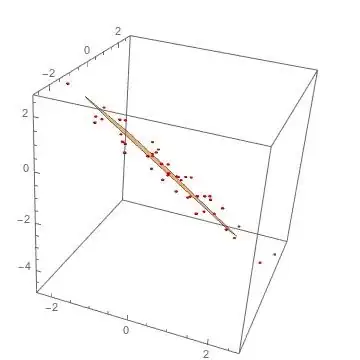
Given points of a planar polygon shape based on point cloud data in 3D space, how can all points that are not on this 2D plane be identified?

e.g.:

enter image description here

The red points represent the values that we know, the orange is the interference. None of the points of the interference are known.

The expected result is an approach to identify all of the points in the same 3D space which are not a part of this 2D shape, based on the points known.

Is there an algorithm or mathematical approach available for solving this type of problem?

I hope that this explanation is clear enough, feel free to comment for further clarification if required.

Many thanks.

Phillip
  • 13
  • Can you find the plane that the black points are in? Is there a predefined origin or do you have to choose one? – CyclotomicField Mar 03 '21 at 13:47
  • I'd try PCA: https://en.wikipedia.org/wiki/Principal_component_analysis and take the plane defined by the eigenvectors corresponding to the two largest eigenvalues. – lhf Mar 03 '21 at 14:46

1 Answers1

1

If we know the red points $p_1,p_2,p_3,p_4$ then we know a close plane to them. Calling this plane $\pi\to a x+b y +c z +d=0$ or $p\cdot \vec n + d=0$ with $p=(x,y,z),\ \ \vec n = (a,b,c)$ we calculate the distances $\lambda_i$ from the points $p_i$ to the plane $\pi$ as follows

$$ (p_i+\lambda_i\vec n)\cdot \vec n + d = 0\Rightarrow \lambda_i = |\frac{d+p_i\cdot\vec n}{\|\vec n\|^2}| $$

rejecting the points with $\lambda_i \gt \lambda_{ref}$

SeedRandom[1]
a = 1; b = 1; c = 1; d = 1;
n = {a, b, c};
p = {x, y, z};
pi = p.n + d;
np = 100;
selected = {};
dataxy = RandomReal[{-2, 2}, {np, 2}];
data = Table[{dataxy[[i, 1]], dataxy[[i, 2]], -(dataxy[[i, 1]] a + dataxy[[i, 2]] b + d)/c } + RandomReal[{-1, 1}, 3], {i, 1, np}];
lambdaref = 0.2;

For[i = 1, i <= np, i++,
 lambda = Abs[d + data[[i]].n]/n.n;
 If[lambda <= lambdaref,
   AppendTo[selected, data[[i]]]
 ]
]


cloud = Table[Graphics3D[{Red, Sphere[data[[i]], 0.04]}], {i, 1, np}];
grselected = Table[Graphics3D[{Red, Sphere[selected[[i]], 0.04]}], {i, 1, Length[selected]}];
gr0 = ContourPlot3D[pi == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Mesh -> False, ContourStyle -> Directive[Orange, Opacity[0.5], Specularity[White, 30]]];
Show[gr0, cloud, PlotRange -> All]
Show[gr0, grselected, PlotRange -> All]

enter image description here enter image description here

Cesareo
  • 36,341