Positioning problem optimal control

Question

Consider the positioning problem: $\dot x_1 = x_2$, $\dot x_2 = u$ with $x_1(0)=0,x_2(0)=X, X>0$. show that the bang-bang control switch can be employed to steer the system to the origin. Find the time taken and the position where the switch must be made.

Answer 1

I am going to do an outline and let you fill in the blanks.

For bang-bang, what are the different choices we should investigate for $u$? They are $\pm 1$. You should note why.

Case 1: $u = 1$

$$x'_1 = x_2$$

$$x_2' = 1$$

with $x_1(0)=0,x_2(0)=X, X>0$.

For this system, we have:

$\tag 1 x_2 x'_2 = x'_1, ~~\text{so}~~ \dfrac{1}{2}\left(x_2^2\right)' = x_1$

If we let $t_0$ belong to the time interval where $u = 1$, and integrate from $t_0$ to $t$, we get:

$$\dfrac{x_2^2(t)}{2} - \dfrac{x_2^2(t_0)}{2} = x_1(t) - x_1(t_0)$$

$$x_2^2(t) = 2 x_1(t) + \left(x_2^2(t_0) - 2x_1(t_0)\right)$$

Using the initial conditions, we have $t_0 = 0$ and this reduces to:

$$\tag 2 x_2^2(t) = 2x_1(t) + X^2 \rightarrow x_2^2(t) = 2x_1(t) + w$$

This tells us that we have a parabola and that as long as $u=1$, the trajectory stays on the curve $(2)$ for some constant $w$.

If we draw the trajectories for this, we have:

Case 2: $u = -1$

Repeat the steps for Case 1, but $u = -1$.

The trajectories look like:

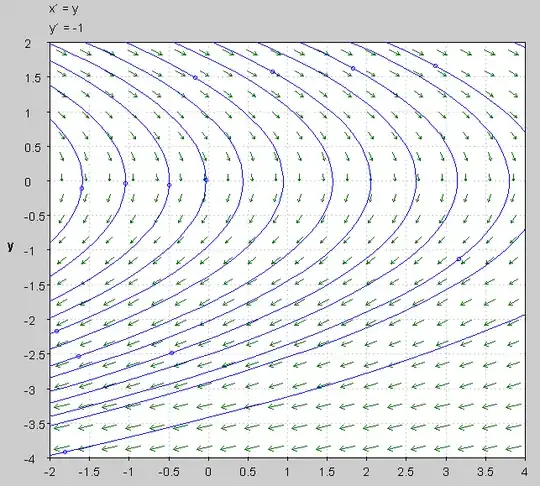
Now that we have analyzed the system for the appropriate values of $u$, we see that the solutions $(x_1(t), x_2(t))$, lie on two different parabolas.

To design an optimal control, we start on one parabola and steer to the origin by starting with $u = -1$ and our trajectory is moving down. We just switch control to $u=1$, which causes us to move to the first parabola and we end up at the origin.

You can work the time portion since you have two parabolas and need to find the time when the switch should occur.