distance point to affine subspace

Question

I have $n$ points $x_i\in\mathbb{R}^N$, $n \le N$. Is there a general formula for the (squared) distance of another point $b$ to the subspace defined by the $x_i$? (Note that I'm not only looking for hyperplanes; the codimension can be larger than 1.)

Answer 1

First move $b$ to the origin, $a_i = x_i - b$, and realize that every point in the plane spanned by the $a_i$ can be written as a linear combination $\sum_i w_i a_i$ with $\sum_i w_i = 1$. The problem can then be formulated as a least-squares problem with an equality constraint, $$ \|A w\|_2^2 \to \min,\\ e^T w = 1 $$ with $A\in\mathbb{R}^{N\times n}$ being the column-vector of the $a_i$ and $e=(1,\dots,1)^T \in\mathbb{R}^n$. This can be solved with a Lagrangian approach, $$ \begin{pmatrix} A^T A & e\\ e^T & 0 \end{pmatrix} \begin{pmatrix} w\\ \lambda \end{pmatrix} = \begin{pmatrix} 0\\ 1 \end{pmatrix} $$ If $A^TA$ is invertible, this gives $$ w = \frac{(A^T A)^{-1}e}{e^T (A^T A)^{-1}e} $$ and $$ \min \|A w\|_2^2 = -\lambda = \frac{1}{e^T (A^T A)^{-1}e}. $$ Note that this expression can never be $0$, so this case is a degeneracy.

---

If not moving $b$ to the origin, the problem is $$ \|A w - b\|_2^2 \to \min,\\ e^T w = 1 $$ and has the solution $$ w = \frac{(A^TA)^{-1}e}{e^T(A^TA)^{-1} e} + \left(ee^T - \frac{(A^TA)^{-1}ee^T}{e^T(A^TA)^{-1} e}\right) (A^TA)^{-1} A^Tb $$ and the distance $$ \min \|A w - b\|_2^2 = \frac{(1 - e^T(A^TA)^{-1} A^T b)^2}{e^T(A^TA)^{-1} e} - b^T A (A^TA)^{-1} A^T b + b^T b. $$ (Perhaps this expression can be further simplified.)

---

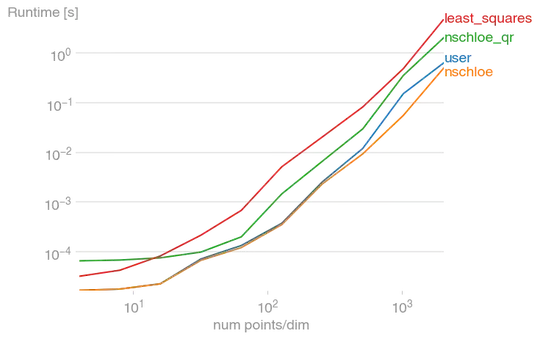
Compared the @user's answer, this one is faster, particularly for large $N$. (Shown here for $n=3$).

Code to reproduce the plot:

import numpy as np
import perfplot
from scipy.linalg import solve_triangular
np.random.seed(0)
def setup(n):
    # k = 3
    k = n
    A = np.random.rand(n, k)
    b = np.random.rand(n)
    e = np.ones(k)
    return A, b, e
def user(Abe):
    A, b, _ = Abe
    V = (A.T - b).T
    V[:, 1:] = (V[:, 1:].T - V[:, 0]).T
    VTV = V.T @ V
    return VTV[0, 0] - VTV[0, 1:].T @ np.linalg.solve(VTV[1:, 1:], VTV[0, 1:])
def nschloe(Abe):
    A, b, e = Abe
    V = (A.T - b).T
    out = 1 / np.sum(np.linalg.solve(V.T @ V, e))
    return out
def nschloe_qr(Abe):
    A, b, e = Abe
    V = (A.T - b).T
    _, r = np.linalg.qr(V)
    w = solve_triangular(r.T, e, lower=True, check_finite=False)
    w = solve_triangular(r, w, check_finite=False)
    out = 1.0 / np.sum(w)
    return out
def least_squares(Abe):
    A, b, _ = Abe
    b -= A[:, 0]
    A = (A[:, 1:].T - A[:, 0]).T
    _, out, _, _ = np.linalg.lstsq(A, b, rcond=None)
    return out[0]
perfplot.show(
    # "out.png",
    setup=setup,
    kernels=[user, nschloe, nschloe_qr, least_squares],
    n_range=[2 ** k for k in range(2, 12)],
    xlabel="num points/dim"
)

Answer 2

As suggested in a comment we may assume that the point $\tilde{x}$ is the origin of coordinates, the coordinates of the other $k+1$ points being $x_0,x_1,\dots x_{k}$. I will assume that the given $k+1$ points span the subspace of dimension $k$ (otherwise the excessive points are removed until the points are linearly independent).

Introducing the vectors $$ v_0=x_0,\quad\forall i=1\dots k:\ v_i=x_i-x_0, $$ an arbitrary point of the subspace defined by $x_i$ can be written as: $$ r=v_0+a_1v_1+\cdots+a_k v_k $$ where $a_i$ are arbitrary real numbers.

We are seeking the vector $a=(a_1,\dots,a_k)$ which minimizes: $$ r^2=(v_0+a_1v_1+\cdots+a_k v_k)^2=a^T Ua+2a^T V+v_0^2,\tag1 $$ where $U$ is symmetric positive definite matrix with elements $U_{ij}=v_i\cdot v_j$ and $V$ is the vector with elements $V_i=v_0\cdot v_i$. As well known the form (1) is minimized by the vector $$ a=-U^{-1}V. $$ Substituting the value into expression (1) one obtains the squared distance to the subspace: $$ r^2=v_0^2-V^TU^{-1}V.\tag2 $$

Answer 3

Move all points such that the plane of the $x_i$ passes through the origin, e.g., $\tilde{x}_i = x_i - x_0$. Every point $y$ in the new plane can be written as $$ y = \sum_i \alpha_i \tilde{x}_i $$ with any $\alpha_i$. This leaves us with the least-squares problem $$ \|b - A\alpha\|^2 \to \min_\alpha $$ where $A$ is the column-matrix of the $\tilde{x}_i$. This can be solved in multiple ways (SVD, QR, normal equation etc.). One possibility is to create an orthogonal basis in the space, e.g., by (modified) Gram-Schmidt, and project $b - x_0$ onto it.