The statement that '$x$, $y$ and $z$ are equivalent' just means
Now suppose its not the case that $x$, $y$ and $z$ are equivalent. That is, suppose:
Under these circumstance, we say that $x$, $y$ and $z$ are what? Inequivalent? This seems wrong, because some of them will still be equivalent.
There is no "special term": We can simply say "not all of $x, y, z$ are equivalent" or "$x, y, z$ are not all equivalent."
As you note, that's not the same thing as all of them being inequivalent, because two of them might still be equivalent, and in the case of logical equivalence, we would need one pair and not all pairs logically equivalent.
Negation of the statement of mutual logical equivalence involves DeMorgan's:
We can say "$x, y, z$" are all equivalent by stating $$(x \iff y) \land (y \iff z)\tag{A}$$ and by transitivity we have also conveyed in $(A)$ that $(x \iff z)$.
And so to negate an entire conjunction, we can arrive at the disjunction of negated dijunctions $$\lnot(x \iff y) \lor \lnot(y \iff z): \tag{$\lnot $ A}$$
$\qquad\qquad\qquad \qquad\qquad\qquad$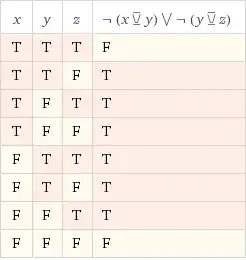
In disjunctive normal form $(\lnot A)$ equivalent to: $$(\lnot x \land y) \lor (\lnot y \land z) \lor (x \land \lnot z)\tag{DNF}$$
And in conjunctive normal form, as you describe in your bullets: we have that $(\lnot A)$ is equivalent to $$(x \lor y\lor z) \land (\lnot x \lor \lnot y \lor \lnot z)\tag{CNF}$$
