There are many, many connections between the trigonometric and hyperbolic functions, some of which are listed here. It is probably too optimistic to expect that a single insight could explain all of these connections, but is there a holistic way of seeing the parallels between $\sin$ and $\sinh$, $\cos$ and $\cosh$? Can all of these seemingly disparate connections be shown to be essentially the same, or at least very similar?
Geometric connections
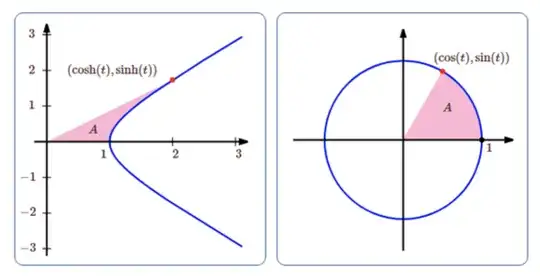
- Sine and cosine parameterise the unit circle $x^2+y^2=1$, just as hyperbolic sine and cosine parameterise the 'unit hyperbola' $x^2-y^2=1$. Both circles and hyperbolas are conic sections.
- The sector of the circle connecting the points $(0,0)$, $(1,0)$, and $(\cos t,\sin t)$ has an area of $t/2$. The region of the hyperbola connecting the points $(0,0)$, $(1,0)$, and $(\cosh t,\sinh t)$ has an area of $t/2$. This can even be used to define the hyperbolic functions geometrically, and many authors do the same with the trigonometric functions.
- Sine and hyperbolic sine are odd, whereas cosine and hyperbolic cosine are even. But sine and cosine are periodic functions, unlike the hyperbolic counterparts.
- The analogue of the identity $\cos^2x+\sin^2x \equiv 1$ is $\cosh^2x-\sinh^2x \equiv 1$. The compound angle formulae are almost identical to their hyperbolic counterparts, save for a pesky minus sign: \begin{align} \sin(x+y) &= \sin(x)\cos(y)+\cos(x)\sin(y) \\ \sinh(x+y) &= \sinh(x)\cosh(y) + \cosh(x)\sinh(y) \\[4pt] \cos(x+y) &= \cos(x)\cos(y) \color{red}{-} \sin(x)\sin(y) \\ \cosh(x+y) &= \cosh(x)\cosh(y) \color{blue}{+} \sinh(x)\sinh(y) \, . \end{align}
- In general, given a trigonometric identity, it is (usually) possible to find a corresponding hyperbolic identity using Osborn's rule: replace every occurrence of $\cos$ with $\cosh$; replace every occurrence of $\sin$ by $\sinh$, but negate the product of two $\sinh$ terms.
Analytic connections
- $\sin$ is the unique solution to the initial value problem \begin{align} f''(x) &= \color{red}{-}f(x) \\ f'(0) &= 1 \\ f(0) &= 0 \, , \end{align} and the corresponding initial value problem for $\sinh$ is the same, except $f''(x) = \color{blue}{+}f(x)$.
- Likewise, the initial value problem for $\cos$ is \begin{align} f''(x) &= \color{red}{-}f(x) \\ f'(0) &= 0 \\ f(0) &= 1 \, , \end{align} and again we see a mysterious sign change for $\cosh$: $f''(x) = \color{blue}{+}f(x)$.
- It follows that the higher-order derivatives of $\sin$ and $\sinh$ form periodic sequences.
- If we solve the initial value problems shown above, we obtain the exponential forms of all $4$ functions: \begin{align} \sin x &= \frac{e^{\color{green}{i}x}-e^{-\color{green}{i}x}}{2\color{green}{i}} \quad{} \cos x = \frac{e^{\color{\green}{i}x}+ e^{-\color{green}{i}x}}{2} \\[3pt] \sinh x &= \frac{e^{x}-e^{-x}}{2} \quad{} \cosh x = \frac{e^x + e^{-x}}{2} \, . \end{align}
- All $4$ functions are analytic, and their Taylor series bear a striking resemblance to each other: \begin{align} \sin x &= x \color{red}{-} \frac{x^3}{3!} + \frac{x^5}{5!} \color{red}{-} \frac{x^7}{7!} + \ldots \\[4pt] \sinh x &= x \color{blue}{+} \frac{x^3}{3!} + \frac{x^5}{5!} \color{blue}{+} \frac{x^7}{7!} + \ldots \\[4pt] \cos x &= 1 \color{red}{-} \frac{x^2}{2!} + \frac{x^4}{4!} \color{red}{-} \frac{x^6}{6!} + \ldots \\[4pt] \cosh x &= 1 \color{blue}{+} \frac{x^2}{2!} + \frac{x^4}{4!} \color{blue}{+} \frac{x^6}{6!} + \ldots \end{align}
- And Euler's formula $$ e^{ix} = \cos x + i \sin x $$ is replaced by the underwhelming $$ e^x = \cosh x + \sinh x \, . $$