Let $X,Y,Z$ be i.i.d $U(0,1)$ random variables. Then $P(X>Y+Z)$

Question

Let $X,Y,Z$ be i.i.d $U(0,1)$ random variables. Then $P(X>Y+Z)$

Saw this question but I am not sure how to utilize it here.

If it was $2$D random variable question I would've easily calculated. $P(X>Y)$ which is inside red outlined shape.

Which is $\dfrac{1}{2}$

but its $3$D now and I am not sure how to setup limits of integration. Since there joint density is unity.

$P(X>Y+Z)=\int_{0}^{1}\int_{?}^{?}\int_{y+z}^{1}1 dxdydz$

Also what other way I can use to solve this ?

One idea here would be to find the distribution of $Y+Z$, and use this to create a similar diagram. The difference will be that, unlike $Y$ or $Z$ individually, their sum will presumably not have a uniform density across the range of possible $Y+Z$. — Semiclassical, Jan 20 '21 at 04:51
@StubbornAtom swear to god when type I dont see it. The one I saw is in question. How do you find questions seriously?But anyways I am looking for a different approach. — DSR, Jan 20 '21 at 04:52
@Semiclassical I can find it using convolution theorem right? — DSR, Jan 20 '21 at 04:53
That'll work. You can also make sense of it intuitively by looking at your blue/red bars in the above plot, and thinking about what the range of allowed $X+Y$ values are. ($Y+Z$ vs. $X+Y$ is just a matter of labeling.) — Semiclassical, Jan 20 '21 at 04:54

Parcly Taxel · Accepted Answer · 2021-01-20T05:01:46.820

2

If we rename the variables so that the problem is $P(Z>X+Y)$, the region of the unit cube $[0,1]^3$ satisfying this condition is a tetrahedron with vertices $(0,0,0),(0,0,1),(0,1,1),(1,0,1)$. The volume of this tetrahedron, hence the final probability since the cube has volume $1$, is $\frac16$.

As an integral this would be $$\int_{x=0}^1\int_{y=0}^x\int_{z=0}^{x-y}1\,dz\,dy\,dx$$ since $X>Y+Z$ implies $X>Y$ and $X-Y>Z$.

edited Jan 20 '21 at 05:01

answered Jan 20 '21 at 04:53

Parcly Taxel

105,904

Thanks for this but I am not aware of $3$D shapes which I couldnt figure out in first place and their volumes. If I have to do this using integrals how do I do it ? – DSR Jan 20 '21 at 04:58
@Daman I have added the integral expression. – Parcly Taxel Jan 20 '21 at 05:02
That is what I was looking for. Last thing, could you please tell me limits if It was that case that $Z>X+Y$ . – DSR Jan 20 '21 at 05:08
@Daman $Z>X+Y$ is just a relabelling, as I said, so the variables change, not the limits! – Parcly Taxel Jan 20 '21 at 05:10
Actually I tried this way but did this thing for $Z>Y+X$ here $Z>Y+X$ implies $Y<-X$ and $\int_{0}^{1}\int_{0}^{-x}\int_{y+x}^{1}dzdydx$ What is wrong here ? – DSR Jan 20 '21 at 05:14
@Daman How can $Y<-X$? That is impossible! – Parcly Taxel Jan 20 '21 at 05:20
I dont know what and how I did it thanks I understood it – DSR Jan 20 '21 at 05:22

score 1 · Answer 2 · answered Jan 20 '21 at 05:14

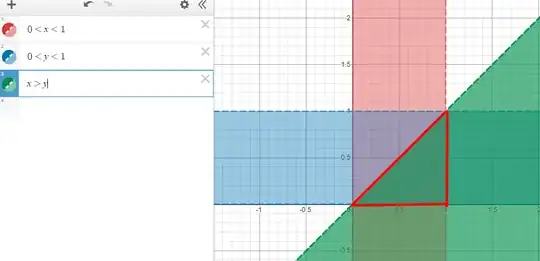
If $Y,Z\sim U(0,1)$ then $S=Y+Z$ is distributed as $$f_S(s)=\left\{\begin{array}{cc} s & 0<s<1\\ 2-s,& 1<s<2,\\ 0&\text{else}\end{array}\right.$$ (See for instance Density of sum of two independent uniform random variables on $[0,1]$. ) For intuition, note that the diagonal range of your blue/red square starts at zero in one corner, rises linearly towards the middle of the square, and then returns to zero. As such, it should be reasonable that $S$ has a triangular distribution.

As such, our problem is now to compute $\text{Pr}(X>S)$ where $X\sim U(0,1)$ and $S$ is distributed as above. The corresponding blue/red picture is similar, but the vertical width of the blue stripe (corresponding to the smaller variable) is $2$ rather than $1$. Moreover, we have to account for the variable density of $S$. Life is made simpler, however, by the fact that we only care about $s<x<1$ and so can take $f_S(s)=s$. Keeping this in mind, we have

$$\text{Pr}(X>S)=\int_{x=0}^1\int_{s=0}^x f_S(s)f_X(x)\,ds\,dx=\int_0^1\int_0^x s^2\,ds\,dx=\int_0^1 \frac13 x^2\,dx=\frac{1}{6}$$ in agreement with the geometric answer.

Let $X,Y,Z$ be i.i.d $U(0,1)$ random variables. Then $P(X>Y+Z)$

2 Answers2