How to prove that this graph is non-planar?

Question

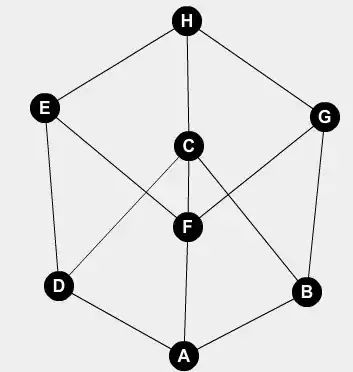
I'm having trouble proving that the above shown graph is non planar, I think that I have to look for a subdivision of the graph $K_{3,3}$ using Kuratowski's theorem, can someone give me any tips to find this?

Answer 1

A good way to visualize $K_{3,3}$ for the purposes of planarity is as a hexagon together with the diagonals connecting opposite vertices.

To find a subdivision of such a thing in a graph, look for a long cycle - here, we might take the cycle $ABCDEHGFA$, for example, which includes all the vertices. Then, look for chords of that cycle that make the $K_{3,3}$ pattern: essentially, you want three edges such that if you draw them all inside the cycle, each one crosses the other two. (One choice, here, is the edges $AD, BG, CF$.) Then if you just take the cycle and those edges, you have a subdivision of $K_{3,3}$.

If the cycle we found did not contain all the vertices, we'd have a tougher time of it, because the other pieces of $K_{3,3}$ don't necessarily have to be single edges, but we could do it.

---

Alternatively, you could notice that the graph you have is bipartite, but all planar bipartite graphs on $n \ge 3$ vertices have $m \le 2n-4$ edges; here, we have $8$ vertices and $13$ edges, and $13 > 2\cdot 8 - 4$.

Answer 2

Consider the cycle $ADEHCF$. The edges between them form $K_{3,3}$ minus the edge $AH$; the path $ABGH$ links $A$ and $H$ without using vertices in the chosen cycle. This is a $K_{3,3}$ minor in the graph, so it is non-planar.