Statistics, Hypothesis and P-value - Check my answers

Question

I am trying to solve a question but stuck with the steps. I can not find any similar questions. With help of some online resources to calculate some parts of the question but I can see that is not enough. I know my approach has lack of information but, this is the only thing I have reached, I was covid ill at the class hours and can not follow the class examples, I thought someone can help me to solve and learn the subject.

With help of the answers from here I try to give an answer. Still need some improvements but tried to do my best. I still do not have answer for question D and confused about CL(the part C) and Significance level(part B)

My answers:

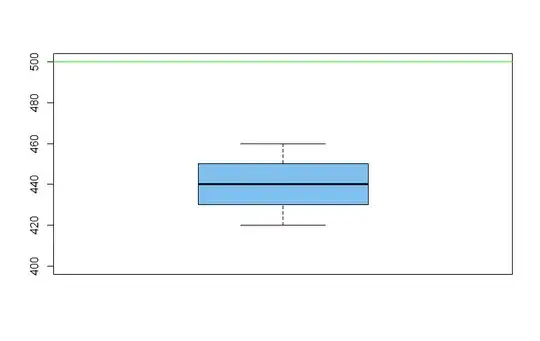
$N\ =\ 9\ \ \ \ \ \ \ \ Sum\ of\ x\ =\ 3970\ \ \ \ \ \ \ \ Mean,\ µ = 441.1111 \ Variance,σ^2 = 161.1111$ $ \sigma\ =\ \sqrt{161.1111} = 12.6929$

$t\ =\ \frac{m\ -\ \mu}{s\ /\ \sqrt n}$

$t\ =\ \frac{500\ -\ 441.1111}{12.6929\ /\ \sqrt9} = 13.918545$

We subtract 1 to get degrees free 9 - 1 = 8

Degrees of freedom = n – 1 = 8

$Probability: P( T ≤ 13.918545) = 0.00000069 $ So, this is the p-Value

$We\ will\ reject\ H_0\ at \ \alpha = 1% $ and also any > 1%

$$ (i) 0.10\ The\ information\ from\ the\ first\ question\, the\ critical\ t-value\ for\ α = 0.10\ and\ df = 8,\ t_c=\ 1.86 \\ CI\ =\ (\bar{X}\ -\ \frac{t_c\ \times\ s}{\sqrt n},\ \bar{\ X}\ +\ \frac{t_c\ \times\ s}{\sqrt n}) \\CI\ =\ (441.1111\ -\ \frac{1.86\ \times\ 12.6929}{\sqrt9},\ \ 441.1111+\frac{1.86\ \times\ 12.6929}{\sqrt9}) = (441.1111 – 7.868, 441.1111 + 7.868) = (433.243, 448.979) $$

$For\ the\ other\ t_c\ values:$

(ii) 0.05 $t_c=\ 2.306$ CL = (431.354, 450.868) (iii) 0.01 $t_c=\ > 3.355$ = (426.915, 455.308)

Based on the answers in part 2 for (i) = 0.90, (ii) = 0.95, (iii) = 0.99, none of the confidence intervals contain 500.

The Question:

The worker says that the mean purchasing cost is 500 USD. We decide to test this.

For a random sample of 9 purchases drawn from a normally distributed population with unknown variance, the costs are:

430, 450, 450, 440, 460, 420, 430, 450, 440.

A) Conduct a hypothesis test of whether the population mean purchasing equals 500 USD. Include all assumptions, the hypotheses, test statistic, and P-value and interpret the result in context.

B) For which significance levels can you reject $H_0?$ (i) 0.10, (ii) 0.05, or (iii) 0.01.

C) Based on the answers in part B), for which confidence levels would the confidence interval contain 500? (i) 0.90, (ii) 0.95, or (iii) 0.99.

D) Use part B) and part C) to illustrate the correspondence between results of significance tests and results of confidence intervals.

Answer 1

I will give some formulas, which may be proved by standard methods.

We have $H_0: X_i \sim N(a, \sigma^2)$,

$a= 500$, $n=9$, $\overline{X} = \frac{\sum_{i=1}^n X_i}{n} = 441.1111...$, $s^2 = \frac{\sum_{i=1}^n (X_i - \overline{X})^2}{n} = \hat{\sigma^2}\frac{n-1}{n}$, $ \hat{\sigma^2} =\frac{\sum_{i=1}^n (X_i - \overline{X})^2}{n-1} = 161.1111...$, $\hat{\sigma} = 12.69296...$.

We know that $\xi_n = \frac{\sqrt{n}(\overline{X} - a)}{\sigma} \sim N(0,1)$, $\eta_n = \frac{ns^2}{\sigma^2} \sim \chi_{n-1}^2$, $\xi_n$ and $\eta_n$ are independent, $$t = \frac{\xi_n}{\sqrt{\frac{\eta_n}{n-1} }} = \sqrt{n-1}\frac{ \overline{X} - a}{s} = \sqrt{n}\frac{ \overline{X} - a}{\hat{\sigma}} \sim T_{n-1}.$$ and also $-t \sim T_{n-1}$, because $T_{n-1}$ is symmetric. Here $T_{n-1}$ is Student's distribution.

We have $t =\sqrt{n}\frac{ \overline{X} - a}{\hat{\sigma}} = -13.9185...$.

If $H_0$ is true then $|t| < u_{\frac{1+\gamma}2}$ with probability $\gamma$, where $u_c$ is a quantile function at $c$.

Put $\gamma = 0.99$. Hence $\frac{1+\gamma}2 = 0.995$. We know that $u_{0.995} = 5.04305...$ and hence $|t| < 5.04305...$ with probability $0.99$, if $H_0$ is true.

Hence we reject $H_0$ for all significance levels in $B$.

The confidence interval for $a$ we get form a condition $$|\sqrt{n}\frac{ \overline{X} - a}{\hat{\sigma}} | < u_{\frac{1+\gamma}2}.$$

It has the form: $$ a \in (\overline{X} - \frac{ u_{\frac{1+\gamma}2}}{\sqrt{n}} \cdot \hat{\sigma} , \overline{X} + \frac{ u_{\frac{1+\gamma}2}}{\sqrt{n}} \cdot \hat{\sigma}).$$

Even in case $\gamma = 0.99$, when the confidence interval is wider, than in cases $\gamma = 0.95$ and $\gamma = 0.90$, we saw that the condition $$|\sqrt{n}\frac{ \overline{X} - 500}{\hat{\sigma}} | < u_{\frac{1+\gamma}2}$$ doesn't hold and hence the confinedce interval doesn't contain $a=500$.

So in $C)$ we get that $500$ is not contained is confinedce interval in any case.

D) We see that $H_0$ is accepted (significance level is fixed) if and only if $a$ is contained in a confidence interval of correspoding confidence level. The correspondence is illustrated.

Addition about D.

$H_0: X_i \sim N(a, \sigma^2)$.

Test has significanse level $1-\gamma$ (in other words, test has level of confidence $\gamma$). Test says that we shoud accept $H_0$ if and only if $$|\sqrt{n}\frac{ \overline{X} - a}{\hat{\sigma}} | < u_{\frac{1+\gamma}2}.$$

The confidence interval has the form: $$ a \in (\overline{X} - \frac{ u_{\frac{1+\gamma}2}}{\sqrt{n}} \cdot \hat{\sigma} , \overline{X} + \frac{ u_{\frac{1+\gamma}2}}{\sqrt{n}} \cdot \hat{\sigma}).$$

So the condition "$a$ belongs to the $\gamma$-confidence interval" is equivalent to condition $$|\sqrt{n}\frac{ \overline{X} - a}{\hat{\sigma}} | < u_{\frac{1+\gamma}2}$$

which is a necessary and sufficient condition to accept $H_0: X_i \sim N(a, \sigma^2)$ with significanse level $1-\gamma$ .

Conclusion. "$a$ belongs to the confidence interval (with level of condidence $\gamma$)" if and only if we accept $H_0: X_i \sim N(a, \sigma^2)$, using the test with significanse level $1-\gamma$ .

Answer 2

As population variance is unknown you have a t-score, not z-score.

I did not check your calculation but if the score is so high (in Absolute value) you will reject the null hypothesis for any significance level.

Thus you reject $H_0$ at $\alpha =1\%$ and also at any $\alpha>1\%$

The rest of the exercise follows as a consequence

Answer 3

Notice that all nine of the observations are \$460 and below? Just from common sense, what does that tell you about the claim that average cost is \$500.

You already have a thoughtful Answer from @tommik (+1), but because you ask I will show some additional detail.

---

Here is a relevant t test from a recent release of Minitab. How much of the output can your find by hand? What parts of the question can you answer from this?

One-Sample T: x
Test of μ = 500 vs ≠ 500
Variable  N    Mean  StDev  SE Mean       95% CI            T      P
x         9  441.11  12.69     4.23  (431.35, 450.87)  -13.92  0.000
Descriptive Statistics: x
Variable  N    Mean  SE Mean  StDev  Minimum      Q1  Median      Q3  Maximum
x         9  441.11     4.23  12.69   420.00  430.00  440.00  450.00   460.00

I don't know whether you are taking this course in a classroom or online. A lot of online courses are using hastily written texts with confusing, useless problems. By contrast, this is a very nice problem carefully written (probably by a real statistician) to encourage your intuitive insight into hypothesis testing and confidence intervals. It will be worth your trouble to do computations, look at results, compare with computer printout, and think carefully about each of your answers.

---

Below is output from R statistical software for the same problem.

x = c(430, 450, 450, 440, 460, 420, 430, 450, 440)
summary(x); length(x);  sd(x)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  420.0   430.0   440.0   441.1   450.0   460.0 
[1] 9        # sample size
[1] 12.69296 # sample SD
t.test(x, mu = 500, conf.lev=.99)
    One Sample t-test


data:  x
t = -13.918, df = 8, p-value = 6.874e-07
alternative hypothesis: 
  true mean is not equal to 500
99 percent confidence interval:
 426.9145 455.3077
sample estimates:
mean of x 
 441.1111
boxplot(x, ylim=c(400,500), col="skyblue2")
 abline(h=500, col="green2")