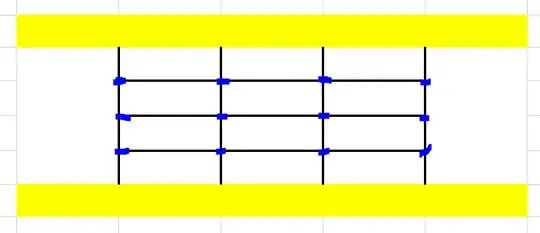
See below chart. The yellow blocks are two islands. It's connected by a grid of cables. There are 16 vertical cables and 9 horizontal cables and 12 nodes (blue highlighted) in between.
Hurricane strike and each cable has 1/2 probability of breaking. Two islands lost contact when there is no path to go from one island to the other on the grid. What's the probability that these two islands lost contact?
I am thinking of something like letting $f(1,1)$ be the probability that the top left node cannot be reached from top island. Then $f(1,1) = 0.5 \cdot (0.5 \cdot (1-f(1,2)) + f(1,2))$. Reason is you need the direct cable from top island to first node broke, and you either need cable from $(1,1)$ to $(1,2)$ broke, or $f(1,2)$ broke. But the equation starts to get a bit messy.
It looks like this might be able to expressed in matrix form or Markov Chain or some sort though..