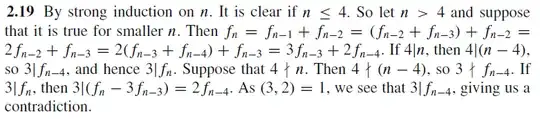Show that $4\mid f_n$ if and only if $6\mid n$.

Question

We define the Fibonacci sequence via $f_1 = f_2 = 1$, and if $n > 2$, then $f_n = f_{n−1} + f_{n−2}$. Show that $4\mid f_n$ if and only if $6\mid n$.

I have been trying to make a copy of the following solution for the exercise "$ 3 \mid f_n $ iff $ 4 \mid n $".

But so far I have not found anything satisfactory. In this question $f_n$ is divisible by $4$ if and only if $n$ is divisible by $6$ they answer it by redefining the fibonacci sequence, but I wonder if it can be done as I am trying. By the way, what they do here $f_n$ is divisible by $4$ if and only if $n$ is divisible by $6$ I don't understand very well.

Answer 1

To expand on this answer, what they've done is considered the sequence modulo $4$. So you have the following sequence:

\begin{align} f_0 &= f_1 = 1\\ f_{n+1} &= f_n + f_{n-1} \bmod 4 \end{align}

(Here I use $\bmod 4$ as a function which returns the remainder in $0, \ldots, 3$.)

Thus, your question is now equivalent to showing that $f_n = 0$ iff $6 \mid n$.

Now, what they note is that the given sequence is periodic with period $6$.

Proving this is not difficult since you can see that $f_1 = f_7$ and $f_2 = f_8$. Now, if two consecutive terms repeat, then everything from that point on must too. (Simply because we have a recursion in terms of the previous two terms.)

Since $f_6 = 0$, we get that $f_{6n} = 0$ for all $n \ge 1$ showing that $n \mid 6 \implies f_n = 0$.

For the converse, note that each of $f_1, \ldots, f_5$ is non-zero and hence, so is each of $f_{6n+1}, \ldots, f_{6n+5}$ for each $n \ge 0$.

Thus, we are done.

Answer 2

As you have asked for, this can be done using a similar argument to the one in your post:

If you repeatedly apply the recurrence relation, then $f_{n} = 8f_{n-5}+5f_{n-6}$ so that when you use strong induction on some set of elements less than $n$ in the same way by supposing $6|n$, then $6|n-6$ and by hypothesis $4|f_{n-6}$ and by the equation above, $4|f_{n}$.

If $6\nmid n$, then $6\nmid (n-6)$ and $4\nmid f_{n-6}$. If $4|f_{n}$, then $4|8f_{n-5}+5f_{n-6}\implies4|5f_{n-6}\implies4|f_{n-6}$, a contradiction. Hence, $4\nmid f_{n}$. In this way, both implications have been shown.

For the second implication, I was unable to use the exact same argument as above since, in this case, $f_{n}$ was not able to reduced in such a convenient way.

Answer 3

You can just go on and see that $$ f_{n+6}=8f_{n+1}+5f_n $$ If $f_n$ is divisible by $4$, then also $f_{n+6}$ is.

If $f_n$ is not divisible by $4$, then neither $f_{n+6}$ is.

(In simpler terms: $f_{n+6}\equiv f_n\pmod{4}$.)

Now just look at $f_0=1,f_1=1,f_2=1,f_3=2,f_4=3,f_5=5$, which is the start of the induction.