3

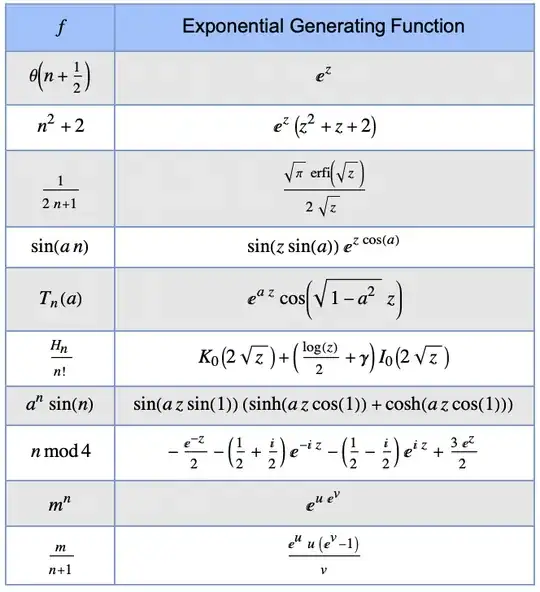
According to my understanding:

  • In differential equations, the input is defined as the entire inhomogeneous part of the equation as it would be written on the right hand side. For example, the input of $y'' + 2y' - t + te^t + y = 0;\ y(0) = 1;\ y'(0) = 1$ is $t - te^t$. When solving for the unit impulse response, this input is to be replaced by $\delta$, yielding $y_{_\delta}'' + 2y_{_\delta}' + y_{_\delta} = \delta;\ y_{_\delta}(0) = 0;\ y_{_\delta}'(0) = 0$.

  • In difference equations, the input is defined as (in general) only part of this inhomogeneous part. For example, given $y[t + 2] - 7y[t + 1] + ty[t] = \cosh(t + 2) - \cosh(t + 1);\ y[0] = 5;\ y[1] = 10$, it cannot be determined whether:

    1. The input is $f[t] = \cosh(t + 2) - \cosh(t + 1)$ and the difference equation has the form $y[t + 2] - 7y[t + 1] + ty[t] = f[t];\ y[0] = 5;\ y[1] = 10$,
    2. The input is $f[t] = \cosh(t)$ and the difference equation has the form $y[t + 2] - 7y[t + 1] + ty[t] = f[t + 2] - f[t + 1];\ y[0] = 5;\ y[1] = 10$,
    3. The input is $f[t] = \cosh(t + 1)$ and the difference equation has the form $y[t + 2] - 7y[t + 1] + ty[t] = f[t + 1] - f[t];\ y[0] = 5;\ y[1] = 10$,

    or any other number of possibilities is correct. The distinction between these possibilities seems to be non-trivial, since when solving for the unit impulse response, only the input is to be replaced by $\delta$, not the entire inhomogeneous part of the difference equation. This leads to the seemingly false conclusion that the difference equation and initial conditions jointly fail to uniquely determine a unit impulse response, that additional information defining the input must be provided.

Since differential equations seem to be limiting cases of difference equations with arbitrarily short time steps, why is there this substantial difference between the two in how the inputs are managed, especially when solving for the unit impulse response?

user10478
  • 2,118
  • Why not define the input as all which is not the homogeneous part? I am assuming that we are handling linear systems, of course. – Cesareo Dec 14 '21 at 19:36
  • @Cesareo This is the way I was taught while studying differential equations (1. in the question). However, it doesn't seem to be the way things are normally done in difference equations, and the discrepancy between the two seems to be more than convention, but a matter of real mathematical significance, i.e., the associated difference equation to find the unit impulse response to 1. will be forced by a single $\delta$ function, while the associated difference equation to find the unit impulse response to 2. and 3. will each be forced by a different sum of $\delta$ functions. – user10478 Dec 14 '21 at 19:53

1 Answers1

1

I am a Mathematica user and know the history of the package rather well. They introduced the difference equations in version 7.0 and the differential equations in the first. So there is a big difference in how interested people are in either.

In DifferenceRoot there is last section that is of high interest to the intent of Your question:

GeneratingFunction[
 DifferenceRoot[
   Function[{y, n}, {-y[n] - y[n + 1] + y[n + 2] == 0, y[0] == 0, 
     y[1] == 1}]][n], n, z]

$$-\frac{z}{-1 + z + z^2}$$

The built-in is DifferenceRoot. The difference equation in this example is the second list to the function. This is in terms of Mathematica Your similarity between difference equation and differential equation. There is not much.

Differential equation are special cases of limit of a difference quotient over time solely. Difference equation are part of the theory of generating functions GeneratingFunction. There are differential equation for generating functions, GeneratingFunction, and difference equations. Both define the generating function complete.

Most generating functions are rational polynoms or transcendential functions.

table of function and generating function

There are too exponential generating functions:

exponential generating functions

Both are mathematics but very different in nature. Do not mix them up.

Mathematica knows some more of this functions categories infinite sums and recurrence equations.

The solution to difference equation are holonomic sequences. The solution to differential equation do not necessarily need to suit more than differentiability of suitable order.

But this is only the Mathematica version. Difference equation appears in very different contexts.

Examples:

  1. Difference_equation as a scheme to set up solvers for differential equations.

  2. The above detailed Mathematica interpretation deals with homogeneous differential equations.

  3. Defnition for scheme for interpolation of functions or data.

  4. The equations in school math with at least one subtraction.

  5. This introduction the relation as in Mathematica with recurrence, What-is-a-difference-equation. ....

    sol = RSolve[{y[n + 2] - 7 y[n + 1] + n y[n] == 0, y[0] == 5, y1 == 10}, y, n]

give a solution in Mathematica. With f there is non.

solution

This is very rapidly increasing.

function plot cosh(+2)−cosh(+1)

This shows the homogeneous function diverges much faster than the inhomogenity does and is pausible that this might be an error in question.

I made use of What is a differnce equation? on google.com

Steffen Jaeschke
  • 905