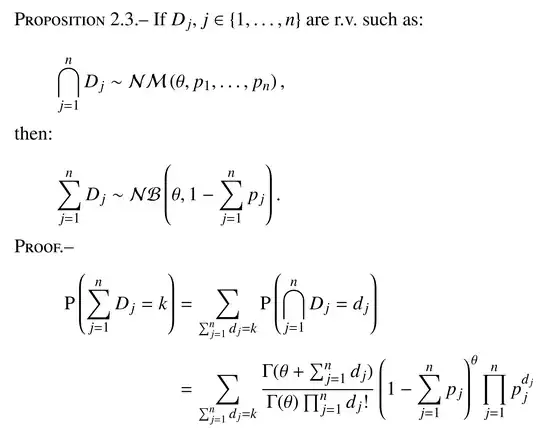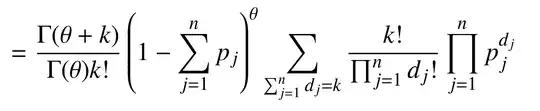0

I have found the formula for the Probability Generating Function of negative multinomial distribution in Definition 8.1 of this chapter (https://onlinelibrary.wiley.com/doi/abs/10.1002/9781118445112.stat01250). It is as follows. $$G_x(\boldsymbol{t}) = \left(\mathcal{Q} - \sum^k_{i=1} P_{it_i}\right)^{-n}$$, where $n > 0$, $P_i > 0(i = i, \ldots, k)$, and $\mathcal{Q} - \sum^k_{i=1} P_{i} = 1$. I am still confused with the following:

  • What do $\mathcal{Q}$ and $P_i$ mean?
  • How can I use this to compute the coefficient of the terms in the series expansion of $\left(x_1, x_2, \ldots, x_m \right)^{-n}$, where, $m > 0$?
Omar Shehab
  • 599
  • 1
    It looks like your source had a typo. I'm guessing the $t_i$ should not have been part of the subscript, so the portion inside the parenthesis should have been $\mathcal{Q} - \sum_{i=1}^k P_i t_i$. Also I've only briefly skimmed it, but this might help: https://math.stackexchange.com/questions/1263942/probability-generating-function-of-a-negative-multinomial-distribution – forgottenarrow Oct 27 '20 at 06:46
  • @forgottenarrow, it is not clear what the size of a multinomial means in that answer. – Omar Shehab Oct 28 '20 at 08:30
  • 1
    I'm not completely sure what you mean by size of a multinomial. That answer seems to be for the case where there are $r+1$ possible events per trial in ${0,1,\dots,r}$ and the trials stop after event 0 appears $k$ times. – forgottenarrow Oct 30 '20 at 19:52
  • 1
    Is the work that you linked published or available somewhere else also? Is it open source? I wanted to read your context from the link but I saw that I would have to purchase the paper... – Noureddine Ouertani Oct 31 '20 at 16:21
  • @NoureddineOuertani, I have shared the screenshots of Section 2.4-5 in the answer which build up to the equation I have mentioned in the question. – Omar Shehab Nov 02 '20 at 15:20
  • Thanks a lot for sharing the screenshots! – Noureddine Ouertani Nov 02 '20 at 17:28

1 Answers1

0

I am using this space to post the content of Section 2.4 which builds up to the equation I have used in the question.

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

Omar Shehab
  • 599