25

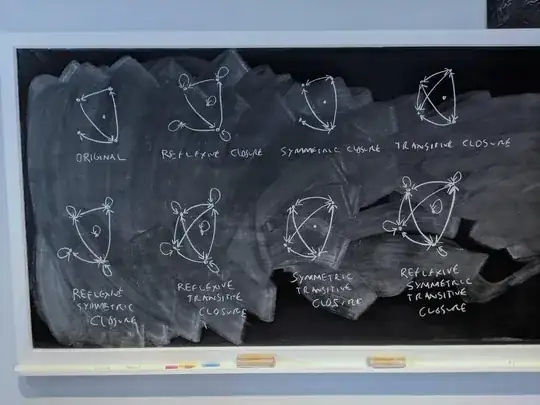
For any given directed graph, we may consider the various closures of it with respect to reflexivity, symmetry, and transitivity, in any combination, like this:

enter image description here

For the particular graph shown above, this process results in eight distinct graphs, including the original graph. This graph is not the smallest instance with this feature, however, since if we delete the source point at right, we will still have eight distinct graphs, like this:

enter image description here

Question. What is the smallest directed graph such that these various closures are all distinct and distinct from the original?

The second example gets it down to five vertices and four edges.

The question arose in a reply of Bryan Bischof to my recent tweet https://twitter.com/JDHamkins/status/1318447368732397569. The first image is drawn from the chapter on Functions and Relations in my book, Proof and the Art of the Mathematics, available from MIT Press: https://mitpress.mit.edu/books/proof-and-art-mathematics.

JDH
  • 45,373
  • One comment that I'll add is that in the above example, you can observe the idempotence of applying the "transitivization" because there's a cycle in the original graph. One could make this a restriction also. – BBischof Oct 20 '20 at 17:38
  • @BBischof Could you explain your comment? All of the operations are idempotent, since they are closure operations: performing them twice is the same as performing them once. But perhaps you mean something else? – JDH Oct 20 '20 at 18:17
  • I agree that their idempotent, my point was that by having a 3-cycle built in, you see that fact immediately from the picture. – BBischof Oct 20 '20 at 19:02
  • 3
    Showing off that your office has a blackboard? Trying to make me jealous? Well, it's working. – Asaf Karagila Oct 21 '20 at 12:45

2 Answers2

26

The $4$-vertex digraph

a ---> b ---> c    d

is the smallest example possible.

To have the reflexive symmetric transitive closure be different from the symmetric transitive closure, we need an isolated vertex. (If a vertex $v$ has an edge to or from it, then in the symmetric transitive closure, we get the edge $v \to v$.) That isolated vertex will make all the reflexive closures different from the non-reflexive ones, but can't help us with anything else.

For the digraph a ---> b ---> c we can check that symmetric, transitive, and symmetric transitive closures are all different. If we want to beat this, we need the same thing to happen on a $2$-vertex digraph.

If the $2$-vertex digraph has edges $a \to b$ and $b \to a$, then its symmetric closure will not change anything. However, if the $2$-vertex digraph does not have both of those edges, then its transitive closure will not change anything. So either way, we need $3$ vertices.

Misha Lavrov
  • 159,700
  • Great! Thanks so much. – JDH Oct 20 '20 at 18:18
  • Incidentally, Chris Hitzel also came up with this graph instance on Twitter at https://twitter.com/HitzelChris/status/1318608158915440645. – JDH Oct 20 '20 at 18:32
0

The graph whose incidence matrix is

0   0   1
0   0   0
0   1   0

has all eight closures distinct. (Or my code has a bug...)

[And given Misha's answer, my code probably has a bug...]

The bug is obvious: the symmetric-transitive closure that Misha and OP were thinking about isn't just the symmetric closure of the transitive closure. You have to apply the two closures alternately until the graph stops changing. D'oh!

But if you interpret "symmetric transitive closure" as the "symmetric closure of the transitive closure" (and similarly for the other terms) then in fact all eight of the named closures are distinct for this graph --- they simply don't account for all possible "closures" (because swapping orders, or repeating things, like STST..., may lead to new ones).

John Hughes
  • 100,827
  • 4
  • 86
  • 159
  • There's some ambiguity. If you take the transitive closure, then take the symmetric closure of that, you get a different digraph from doing the two operations in the other order. (Or we could take the fixed point.) – Misha Lavrov Oct 20 '20 at 17:56
  • Right -- I was thinking that "the trnasitive symmetric closure" doesn't make sense because of the word "the" ... unless you use the fixed-point definition. Either that, or there are more than 8 possible combinations, because ST and TS might yield different graphs, etc. :) – John Hughes Oct 20 '20 at 18:41
  • The transitive-symmetric closure of a relation R is defined to be the smallest relation extending R that is both transitive and symmetric. And similarly with the other closure notions. This is distinct from the symmetric closure of the transitive closure. – JDH Oct 20 '20 at 19:52
  • But I guess it is the same as the transitive closure of the symmetric closure, so you don't need to iterate if you simply do it in the other order, right? – JDH Oct 20 '20 at 19:58
  • 3
    I think that's right (that trans(sym(R)) is the trans-sym closure; it's certainly transitive. And because the thing on which trans is applied is already symmetric, if edge A->B gets added, then B->A also gets added, etc.., etc. I didn't really think through all the possibilities --- it's like that topology question about "Given a subset of the real line and the operations "closure" and "complement", how many different sets can possibly be generated?" I don't know how many distinct sequences-of-closure-operations can generate different things....but I'm not going to try to learn, either. – John Hughes Oct 20 '20 at 20:25
  • Ok, now I'm getting interested in this question as well. It seems like the substructures that lead to these chains are probably classifiable, and the length before they converge is pretty bounded by number of nodes. – BBischof Oct 20 '20 at 20:42
  • 1
    OK. I've posed it as its own question: https://math.stackexchange.com/questions/3874256/closure-sequence-lengths-in-graphs – John Hughes Oct 20 '20 at 21:00