1

In the lecture on boolean schemes, I was stuck with the following inequality: for any $c<2$ there exists N (big enough), such that for any $n>N: c^n\log_{2}\left(c^n\right)<2^n$. I want to prove it. It might be also that our prof was wrong. Please help to solve the problem. It looks unbelievable to me since the limit of the lefthand side is $n2^n>2^n$ when $c→2$. But I understand that it might be true since $c$ is fixed.

robjohn
  • 353,833
Sergey Bond
  • 127

2 Answers2

1

The inequality can be rewritten

$$n\log_2 c<\left(\dfrac 2c\right)^n,$$ where the ratio exceeds $1$. It is well known that any polynomial (here a linear one) grows slower than an exponential, hence the claim.

For a more explicit justification, take the ratio of the terms $n+1$ and $n$ both in the LHS and RHS.

$$\text{LHS}\to1+\frac1n,\\\text{RHS}\to \frac2c.$$

Then for $n>\dfrac c{2-c}$ the LHS is bounded above by a geometric progression of a smaller common factor then the RHS.

Numerical example:

Let us consider $c=1.9$ and $n\ge20$. Then we can write

$$LHS=O(1.05^n)$$ while

$$RHS=\left(\frac2{1.9}\right)^n=1.0526\cdots^n.$$

  • I understood your 1st proof. Thank you! There is a proof of your claim online.https://math.stackexchange.com/questions/55468/how-to-prove-that-exponential-grows-faster-than-polynomial – Sergey Bond Sep 29 '20 at 08:31
  • I guess I figured out what you ment by the second part $$\log_{2}\left(c^n\right)<(2/c)^n$$ $$(n\log_{2}\left(c\right))^{1/n}<(2/c)$$ $$n^{1/n}(log_{2}\left(c\right))^{1/n}<(2/c)$$ The $LHS→1$ since $n^{1/n}→1$ and $a^{1/n}→1$ when $a>0$ and $n→infinity$ – Sergey Bond Sep 29 '20 at 09:26
  • @SergeyBond: this is not at all what I expressed. I referred to the ratio of successive terms and used a comparison with geometric sequences. I have added an example. –  Sep 29 '20 at 10:33
1

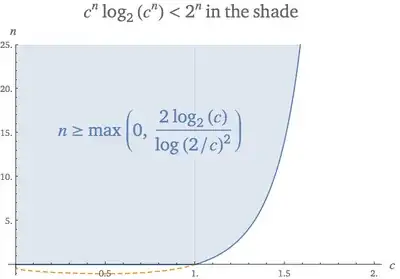
Problems arise unless we also assume that $c\gt0$. Note that if $c\le1$, then the left side of $$ c^n\log_2\left(c^n\right)\lt2^n\tag1 $$ is non-positive, and so $(1)$ is trivially true.

All that is left is to prove $(1)$ for $1\lt c\lt2$. In this range, $\log_2(c)$ and $\log(2/c)$ are both positive.

Dividing $(1)$ by $c^n$ shows that $(1)$ is equivalent to $$ n\log_2(c)\lt\left(\frac2c\right)^n=e^{n\log(2/c)}\tag2 $$ Whenever $n\ge\frac{2\log_2(c)}{\log(2/c)^2}$, we have $$ \begin{align} e^{\color{#C00}{n\log(2/c)}} &\gt\frac12(\color{#C00}{n\log(2/c)})^2\tag3\\ &\ge n\log_2(c)\tag4 \end{align} $$ Explanation:
$(3)$: $e^x\gt\frac12x^2$ by the Taylor Series for $e^x$
$(4)$: $n\ge\frac{2\log_2(c)}{\log(2/c)^2}$

Inequality $(4)$ says that inequality $(2)$, which is equivalent to inequality $(1)$, holds when $n\ge\frac{2\log_2(c)}{\log(2/c)^2}$. Summarizing,

For any $c\in(0,1]$ and $n\ge0$, or $c\in(1,2)$ and $n\ge\frac{2\log_2(c)}{\log(2/c)^2}$, we have $$ c^n\log_2\left(c^n\right)\lt2^n\tag5 $$

enter image description here

robjohn
  • 353,833
  • This answer avoids the asymptotic ($\sim$) and big-O estimates by giving concrete bounds on how big $n$ needs to be for a given $c$ to satisfy $(1)$. – robjohn Sep 30 '20 at 17:27