What is the intuition behind the trace of an endomorphism?

Question

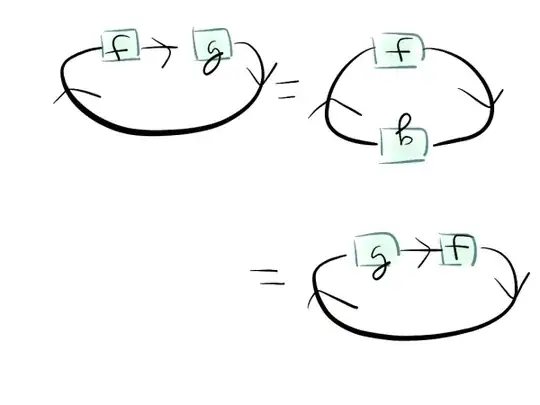
Looking back on my math education, I noticed that even though the trace of an endomorphism came up a lot, I'd be hard pressed to give a good description of what the trace really means. I'm looking for some good intuition about its meaning.

To elaborate on what I'm looking for: if I forgot the rigorous definition of the determinant, I could rebuild it from scratch without reference to a basis because I know that it's supposed to measure the change in volume and orientation of a parallelepiped under a linear transformation. For the same reason, I can quickly tell that it is independent of basis, multiplicative, and determines wether the endomorphism is injective or not, all without doing any calculations. I want something similar for the trace. It doesn't need to be geometric, but I want to know what the trace tells us about how the endomorphism acts.

Answer 1

For finite-dimensional vector spaces $V$, there is a canonical isomorphism of $V$ with its double dual $V^{**}$ and this makes the vector space $V \otimes V^*$ naturally isomorphic to its own dual space: $$ (V \otimes V^{*})^* \cong V^* \otimes V^{**} \cong V^* \otimes V \cong V \otimes V^{*}, $$ where the first and last isomorphisms are the natural ones involving tensor products of (finite-dimensional) vector spaces. Since $V \otimes V^{*} \cong {\rm End}(V)$, we get that ${\rm End}(V)$ is naturally isomorphic as a vector space to its own dual space. If you unwrap all of these isomorphisms, the isomorphism ${\rm End}(V) \to ({\rm End}(V))^{*}$ sends each linear operator $A$ on $V$ to the following linear functional on operators on $V$: $B \mapsto {\rm Tr}(AB)$. In particular, the identity map on $V$ is sent to the trace map on ${\rm End}(V)$.

Answer 2

One way to think about it is that the trace is the unique linear map with the property

$$\operatorname{tr}(|u\rangle\langle v|) = \langle u | v\rangle $$

In particular in the case of a rank 1 matrix $A=\lambda|u\rangle\langle v|$ we see that the trace in some sense measures "how much $\ker(A)^\perp$ is aligned with $\operatorname{Im}(A)$". Does this viewpoint carry over to matrices that are not rank-1?

Consider a higher rank matrix $A=\sum_{i=1}^k \sigma_i|u_i\rangle\langle v_i|$. Again we may assume $u_i$ and $v_i$ are normalized (you may notice that when $k=n$ and the $u_i$ and $v_j$ are orthogonal this is the SVD of $A$) then

$$\operatorname{tr}(A)= \operatorname{tr}(\sum_i \sigma_i|u_i\rangle\langle v_i|) = \sum \sigma_i\langle v_i|u_i\rangle $$

Which is a weighted sum of how much the orthogonal complements of the kernels of the rank-1 components align with their images. Due to linearity, it does not matter how we represent $A$ as a sum of rank-1 matrices.

Notable special cases:

• if $A$ has an orthogonal eigenbasis, then $A=\sum_i \lambda_i |v_i\rangle\langle v_i|$ and so $\operatorname{tr}(A)=\sum_i\lambda_i\langle v_i|v_i\rangle = \sum_i \lambda_i$. Here the orthogonal complements and the images of the rank 1 components are perfectly aligned.

• For a projection matrix $P$ (i.e. $P^2=P$) we have $\operatorname{tr}(P)=\dim \operatorname{Im}(P)$. Since $P$ acts like an identity on the subspace is projects onto, again the orthogonal complements of the kernel and the image are perfectly aligned.

• For a nilpotent matrix $N$, the trace is zero. In fact, we can write $N$ as a sum of rank-1 matrices where the orthogonal complement of the kernel is orthogonal to the image for each of them. (can be proven for example via Schur decomposition)

Answer 3

Here's a cute geometric interpretation: the trace is the derivative of the identity at the origin. That is, we have

$$\det (1 + At) = 1 + \text{tr}(A) t + O(|t|^2)$$

So if you think of the determinant geometrically in terms of volumes, the trace is telling you something about how a matrix very close to the identity changes volumes. Similarly we have the identity

$$\det \exp(At) = \exp(\text{tr}(A) t).$$

This identity explains, among other things, why the Lie algebra of the special linear group $SL_n$ is the Lie algebra $\mathfrak{sl}_n$ of matrices with zero trace.

The argument in KCd's answer can be substantially generalized and you can get some pretty pictures out of it. There is a way of defining the trace using what are called string diagrams which, among other things, makes it immediately clear why the trace satisfies the cyclicity property $\text{tr}(AB) = \text{tr}(BA)$ (note that this is at least apparently slightly stronger than being conjugation-invariant): see this blog post and this blog post. As a teaser, once the appropriate notation has been introduced and the appropriate lemmas proven, here is a complete proof of cyclicity:

Answer 4

Here's one characterization of trace that deserves to be more well-known. It's standard that everyone knows that $\det T$ for a linear transformation $T$ can be characterized as $$(\det T) v_1\wedge...\wedge v_n=Tv_1\wedge...\wedge Tv_n$$ for every basis $v_1,...,v_n\in V$. Trace has a similar characterization, namely under the same hypothesis, $\text{tr}T$ can be defined as the unique number such that $$(\text{tr}T)v_1\wedge...\wedge v_n=\sum_{i=1}^n v_1\wedge...\wedge Tv_i\wedge...v_n.$$ From this characterization, it's believable that trace and det related via taking derivatives by product rule; indeed, that is the case as seen in the following identity $$\partial_s\det(T_s)=\det(T_s)\text{tr}(T_s^{-1}\partial_s T_s),$$ where $T_s$ is a path in $\text{Iso}(V)$.

Answer 5

The trace of a finite-dimensional $k$-vector space $V$ is the composition $$\mathrm{End}(V)\xleftarrow\sim V^\vee\otimes V\xrightarrow{\mathrm{ev}}k,$$ where $V^\vee\otimes V\to \mathrm{End}(V):v^\vee\otimes v\mapsto (w\mapsto v^\vee(w)v)$ is an isomorphism, and $\mathrm{ev}\colon V^\vee\otimes V\to k:v^\vee\otimes v\mapsto v^\vee(v)$ is the evaluation homomorphism.

Answer 6

There are many great answers here. Here is one more, very elementary one. Let $k$ be a field, and let $k^{n\times n}$ denote the space of $n \times n$ matrices with coefficients in $k$.

Lemma The kernel of the trace operator, regarded as a linear map $k^{n\times n} \to k$, is the space of commutators $\mathrm{Com}(k,n) = \{AB - BA : A, B \in k^{n\times n}\}$.
Proof There are several proofs for this; K. Shoda (1936) Japan J. Math. 13 361-5 gave an argument that works for fields of finite characteristic. A.A. Albert and B. Muckenhoupt (1957) Michigan Math. J. 4 1-3 establishes the claim for any characteristic. Kahan gives a nice argument, though I'm not sure this was vetted in peer review.

Definition The trace operator $\mathrm{tr}:k^{n\times n} \to k$ is the unique linear map such that $\mathrm{Ker}(\mathrm{tr}) = \mathrm{Com}(k,n)$ and $\mathrm{tr}(I) = n$, where $I$ denotes the $n \times n$ identity matrix.

Answer 7

Let $f:U\subset \mathbb R^n\to\mathbb R^n$ be a $C^1$ vector field, then the trace of differential of $f$ (or trace of jacobian matrix), is equal to, the divergence of $f$. Explicitly, $$\operatorname{trace}\big(df|_p\big)=\operatorname{trace}\left(\array{\frac{\partial f^1}{\partial x^1} & \cdots & \frac{\partial f^1}{\partial x^n}\\ \vdots & \ddots & \vdots \\ \frac{\partial f^n}{\partial x^1}& \cdots & \frac{\partial f^n}{\partial x^n}}\right)|_p=\sum_{i=1}^n \frac{\partial f^i}{\partial x^i}|_p=\operatorname{div} f|_p$$ And divergence is coordinate free in the sense of Euclid inner space $\mathbb R^n$ or $\operatorname{SO}(n)$, because $$\operatorname{div} f|_p=\lim_{r\to 0}\frac{1}{\operatorname{Vol}(U_r)}\int_{\partial U_r} \langle f,\mathbf{n} \rangle(x)\, dx$$ where (1) $U_r$ can be a $r$-radius ball or rectangle that center at $p$, (2) $\mathbf{n}$ is outer unit normal vector of surface $\partial U_r$ at $x$, (3) $\langle f,\mathbf{n} \rangle(x)$ is the inner product at $x\in \partial U_r$, (4) surface integral.