On an infinitely large chessboard, in how many paths of length $10$ can a knight take and end up in its original position?

Question

The knight is moved exactly $10$ times. A knight has $8$ possible ways to move once. So I believe there are $8^{10}= 2^{30} \sim 1$ billion permutations. How many in which the knight ends up on the same square?

Answer 1

Here is an approach using multivariate generating functions, although the final evaluation is a bit impractical without a computer, it is doable. This approach also allows for generalization to other pieces/movements and ending positions (well as long as we have finite number of possibilities for movement, of course).

Let's encode the positions in two dimensions with integer coordinates and say we start at $(0,0)$. Let $f(x,y)=\sum a_{i,j} x^iy^j$ where $a_{i,j}$ is $1$ if the piece can get to $(i,j)$ on first move, and $0$ otherwise. Then number of ways the piece can be at any position $(i,j)$ after $n$ moves is coefficient of $x^iy^j$ in $f(x,y)^n$. This is because multiplying of individual terms translates into addition on the exponents, and also because we start at $(0,0)$ (so by addition/subtraction of the first moves we generate all subsequent moves).

For the knight, the viable first moves are $(i,j)\in \{(\pm 1, \pm2), (\pm 2, \pm 1)\}$, and so $$f(x,y)=xy^2+x^2y+x^{-1}y^2+x^2y^{-1}+xy^{-2}+x^{-2}y+x^{-1}y^{-2}+x^{-2}y^{-1}.$$

So the number of ways the knight will end at position $(0,0)$ after $10$ moves is coefficient of $x^0y^0=1$ (constant) in $f(x,y)^{10}$. Now we can either use computer algebra system such as Maple to evaluate the polynomial and extract the corresponding coefficient, or we can further apply little algebra and notice $$ g(x,y)=x^2y^2f(x,y)=x(x^2+1)(y^4+1)+y(y^2+1)(x^4+1), $$ and that we are interested in coefficient of $x^{20}y^{20}$ in $g(x,y)^{10}$. Using the binomial theorem repeatedly, we can see that this is sum of all possible $$\binom{10}{k}\binom{k}{i_1}\binom{10-k}{j_1}\binom{k}{i_2}\binom{10-k}{j_2},$$ where $k+2i_1+4j_1=20,10-k+4i_2+2j_2=20$ and $k,i_1,i_2,j_1,j_2\geq 0$. The conditions imply that $k$ is even, so we want to evaluate: $$ \sum_{\substack{k,i_1,i_2,j_1,j_2 \geq 0\\i_1+2j_1=10-k\\2i_2+j_2=5+k}} \binom{10}{2k}\binom{2k}{i_1}\binom{10-2k}{j_1}\binom{2k}{i_2}\binom{10-2k}{j_2}. $$

We can further notice things that $\sum \binom{2k}{i_1}\binom{10-2k}{j_1}$ and $\sum \binom{2k}{i_2}\binom{10-2k}{j_2}$ can be evaluated independently and that they are same for $k$ and $5-k$, which slightly reduces the number of terms. Eventually you will only need to evaluate binomial coefficients $\binom{10}{5}$, $\binom{10}{4}$, $\binom{10}{2}$, $\binom{8}{4}$, $\binom{8}{2}$, $\binom{6}{3}$, $\binom{6}{2}$, $\binom{4}{2}$ (not mentioning obvious values of $\binom{m}{0}$ and $\binom{m}{1}$), so it's not that bad.

In any way, at some point in the simplification it becomes matter of calculation, I suggest to look at bof's answer for the way to do it nicely using pencil & paper way. Notice that both answers arrived at the basically the same sum by different means (one algebraic, the other one more combinatoric).

Following code can be used for evaluation in Maple:

N := 10:
S := 0:
for k from 0 to N/2 do: 
  term := binomial(N, 2*k): 
  term := term * add(binomial(2*k, N-k-2*j1)*binomial(N-2*k, j1), j1=0..(N-k)/2):
  term := term * add(binomial(2*k, i2)*binomial(N-2*k, N/2+k-2*i2), i2=0..(N/2+k)/2): 
  S := S + term 
od:
S;

or

N := 10:
coeff(coeff((x*y^2+x^2*y+y^2/x+x^2/y+x/y^2+y/x^2+1/(x*y^2)+1/(x^2*y))^N, x, 0), y, 0);

Output:

13180608

Answer 2

Here is a formula for the number of closed walks of length $2T$ by a knight on an infinite chessboard, beginning and ending on a given square: $$\sum_{m+n=T}\binom{2T}{2m}\left[\sum_{h+2k=m+2n}\binom{2m}h\binom{2n}k\right]\left[\sum_{2h+k=2m+n}\binom{2m}h\binom{2n}k\right]$$ Explanation. Call a knight move "(mostly) horizontal" if it's two squares left or right and one square up or down, "(mostly) vertical" if it's one square left or right and two squares up or down. In order for the knight to return to its starting square, it must make an even number of horizontal moves and an even number of vertical moves, say $2m$ horizontal moves and $2n$ vertical moves, where $2m+2n=2T$ or more simply $m+n=T$.

The factor $\binom{2T}{2m}$ is the number of ways we can permute the $2m$ horizontal moves $(\pm2,\pm1)$ and the $2n$ vertical moves $(\pm1,\pm2)$.

The factor $\sum_{h+2k=m+2n}\binom{2m}h\binom{2n}k$ is the number of ways we can attach signs to the vertical (second) coordinates so that the net vertical displacement is zero. Namely, the total (unsigned) vertical distance traveled by the knight in making $2m$ horizontal and $2n$ vertical moves is $2m+4n$; so we have to attach $+$ signs to the second coordinates of $h$ of the $2m$ horizontal moves and $k$ of the $2n$ vertical moves, and $-$ signs to the rest, where $h+2k=(2m+4n)/2=m+2n$.

Likewise, the factor $\sum_{2h+k=2m+n}\binom{2m}h\binom{2n}k$ is the number of ways we can attach signs to the horizontal (first) coordinates so that the net horizontal displacement is zero.

Calculation. To find the number of closed knight walks of length $10$, we set $T=5$.

$m=0$, $n=5$:

$$\binom{10}0\left[\sum_{h+2k=10}\binom0h\binom{10}k\right]\left[\sum_{2h+k=5}\binom0h\binom{10}k\right]$$ $$=\binom{10}0\left[\binom00\binom{10}5\right]\left[\binom00\binom{10}5\right]=63504.$$ $m=1$, $n=4$: $$\binom{10}2\left[\sum_{h+2k=9}\binom2h\binom8k\right]\left[\sum_{2h+k=6}\binom2h\binom8k\right]$$ $$=\binom{10}2\left[\binom21\binom84\right]\left[\binom22\binom82+\binom21\binom84+\binom20\binom86\right]=1234800.$$ $m=2$, $n=3$: $$\binom{10}4\left[\sum_{h+2k=8}\binom4h\binom6k\right]\left[\sum_{2h+k=7}\binom4h\binom6k\right]$$ $$=\binom{10}4\left[\binom40\binom64+\binom42\binom63+\binom44\binom62\right]\left[\binom43\binom61+\binom42\binom63+\binom41\binom65\right]=5292000.$$ $m=3$, $n=2$: $$\binom{10}6\left[\sum_{h+2k=7}\binom6h\binom4k\right]\left[\sum_{2h+k=8}\binom6h\binom4k\right]=5292000.$$ $m=4$, $n=1$: $$\binom{10}8\left[\sum_{h+2k=6}\binom8h\binom2k\right]\left[\sum_{2h+k=9}\binom8h\binom2k\right]=1234800.$$ $m=5$, $n=0$: $$\binom{10}{10}\left[\sum_{h+2k=5}\binom{10}h\binom0k\right]\left[\sum_{2h+k=10}\binom{10}h\binom0k\right]=63504.$$ Final answer: $$63504+1234800+5292000+5292000+1234800+63504=\boxed{13180608}$$ which agrees with the value at A254129.

Answer 3

Here is a little program to compute it:

from collections import defaultdict
d = int(input('Number of moves: '))
dx = [2, 1, 2, 1, -2, -1, -2, -1]
dy = [1, 2, -1, -2, 1, 2, -1, -2]
pos = defaultdict(int)
pos[0, 0] = 1
for _ in range(d):
    new = defaultdict(int)
    for (x, y), c in pos.items():
        for l in range(8):
            nx = x + dx[l]
            ny = y + dy[l]
            new[nx, ny] += c
    pos = new
print(pos[0, 0])

It produces the right answer for 10 immediately and also for 100 in about 10s.

Answer 4

A quick approximation, which should at least give the right asymptotics, using probability. Let the coordinates be $X_n=\sum_n x_i$ and $Y_n=\sum_n y_i$ where $x_i$ and $y_i$ are random variables taking values on $\{-2, -1, 1, 2\}$ with equal probability. $x_i$ and $x_j$ are independent, but $x_i$ and $y_i$ are not - they are uncorrelated, however. Then, we can expect that, for large even $n$, the CLT applies and $(X,Y)$ can be approximated by a joint gaussian (uncorrelated, hence independent) taking values over the even coordinates ($X+Y=0 \pmod 2$).

Further, $E[x_i]=E[y_i]=0$ and $E[x_i^2]=E[y_i^2]=\sigma^2=\frac52$

Hence, using the zero order approximation $\int_{-1/2}^{1/2} f(x) dx \approx f(0)$ $$P( X_{10}=0,Y_{10}=0) \approx 2 \frac{1}{2 \pi 10 \sigma^2}=0.01273 \tag{1}$$

And then the number of paths is approximately

$$ 0.01273 \times 8^{10}=13671306\tag 2$$

In general, the number of paths in this approximation is $$C_n \approx \frac{2}{5 \pi \, n} \, 8^n \qquad n \text{ even}\tag3$$

The error of $(2)$ wrt the exact value ($13180608$) is around $3.7\%$.

One should expect this approximation to improve with $n$ (moves) increasing. For example, for $n=24$ the relative error is around $2 \%$.

Empirically, the asympotic seems to be

$$C_n = \frac{2}{5 \pi \, n} \, 8^n \left(1 - \frac{1}{2n}+o(n^{-1}) \right)\tag4$$

---

Edit: Now I see that $(3)$ is mentioned in https://oeis.org/A254129 - I don't know if this probabilistic approach was used.

Answer 5

In the answer by @Sil it is shown that then number is the constant term of $$p(x,y)=(xy^2+x^2y+x^{-1}y^2+x^2y^{-1}+xy^{-2}+x^{-2}y+x^{-1}y^{-2}+x^{-2}y^{-1})^{10}$$ We sill see here that this can be used to calculate the result without a calculator.

We have $$p(x,y)=\left(x+\frac 1 x \right)\left(y^2+\frac 1 {y^2}\right)+\left(y+\frac 1 y\right)\left(x^2+\frac 1 {x^2}\right)$$ and, if we substitute $$u=x+\frac 1 x $$ $$v=y+\frac 1 y $$ $$p(x,y)=\left(u(v^2-2)+v(u^2-2)\right)^{10}\\=\sum_{k=0}^{10} {10 \choose k} u^k(v^2-2)^kv^{10-k}(u^2-2)^{10-k}$$ If $c(\text{series})$ is the constant term of a series, then $$c(s_1(x)\cdot s_2(y))=c(s_1(x))\cdot c(s_2(y))$$ $$c(s_1(x)+s_3(x))=c(s_1(x))+c(s_3(x))$$ $$c(s_4(x))=0,\text{if }s_4\text{ contains only odd powers of } x$$

Further we have $$u^{2k}=(x+\frac 1 x)^{2k}=\frac{((x+1)^2)^k} {x^k}$$ and therefore $$c(u^{2k})={ 2k \choose k}$$ So we have $$c(p(x,y))=\sum_{k=0}^{5} {10 \choose 2k} c(u^{2k}(u^2-2)^{10-2k})c((v^2-2)^{2k}v^{10-2k})\\ =\sum_{k=0}^{5} {10 \choose 2k}\left(\sum_{l=0}^{10-2k}{10-2k \choose l} c(u^{2k+2l})(-2)^{10-2k-l}\right)\left(\sum_{l=0}^{2k}{2k \choose l} c(v^{10-2k+2l})(-2)^{2k-l}\right)\\ =\sum_{k=0}^{5} {10 \choose 2k}\sigma(5-k)\sigma(k)$$

where $$\sigma(k)=\sum_{l=0}^{2k}{2k \choose l} c(v^{10-2k+2l})(-2)^{2k-l}$$ or $$\sigma(k)=\sum_{l=0}^{2k}{2k \choose l} {10-2k+2l \choose 5-k+l}(-2)^{2k-l}$$

The generalisation to $2T$ moves is obviously

$$\sum_{k=0}^{T} {2T \choose 2k}\sigma(T-k)\sigma(k)$$ where $$\sigma(k)=\sum_{l=0}^{2k}{2k \choose l} {2(T-k+l) \choose T-k+l}(-2)^{2k-l}$$

Calculating the numbers by hand

The binomial coefficients can be calculated recursively (Pascal's Triangle):

\begin{matrix} &&&&&&&&&&1&\ldots\\ &&&&&&&&&1&&\ldots\\ &&&&&&&&1&&2&\ldots\\ &&&&&&&1&&3&&\ldots\\ &&&&&&1&&4&&6&\ldots\\ &&&&&1&&5&&10&&\ldots\\ &&&&1&&6&&15&&20&\ldots\\ &&&1&&7&&21&&35&&\ldots\\ &&1&&8&&28&&56&&70&\ldots\\ &1&&9&&36&&84&&126&&\ldots\\ 1&&10&&45&&120&&210&&252&\ldots \end{matrix}

We need the values $c(v^0), c(v^2), c(v^4), c(v^6), c(v^8), c(v^{10})$ These values can be easily calculated recursively.

The values $c{2k \choose k}$ can be calculated in the following way:

$$\begin{matrix}{0 \choose 0}&=&1\\ {2 \choose 1}&=&2\\ {4 \choose 2}&=&6\\ {6 \choose 3}&=&20\\ {8 \choose 4}&=&70\\ {10 \choose 5}&=&{8 \choose 4}\cdot \frac {2\cdot 9}5&=&252\\ {12 \choose 6}&=&{10 \choose 5}\cdot \frac {2\cdot 11}6&=&924\\ {14 \choose 7}&=&{12 \choose 6}\cdot \frac {2\cdot 13}7&=&3432\\ {16 \choose 8}&=&{14 \choose 7}\cdot \frac {2\cdot 15}8&=&12870\\ {18 \choose 9}&=&{16 \choose 8}\cdot \frac {2\cdot 17}9&=&48620\\ {20 \choose 10}&=&{18 \choose 9}\cdot \frac {2\cdot 19}{10}&=&184756 \end{matrix} $$

Now we calculate $\sigma(5)$. All other values of sigma can be calculated in a similar way and need less terms.

$$ \sigma(5)={10 \choose 0}{0 \choose 0}(-2)^{10}\\ +{10 \choose 1}{2 \choose 1}(-2)^{9}\\ +{10 \choose 2}{4 \choose 2}(-2)^{8}\\ +{10 \choose 3}{6 \choose 3}(-2)^{7}\\ +{10 \choose 4}{8 \choose 4}(-2)^{6}\\ +{10 \choose 5}{10 \choose 5}(-2)^{5}\\ +{10 \choose 6}{12 \choose 6}(-2)^{4}\\ +{10 \choose 7}{14 \choose 7}(-2)^{3}\\ +{10 \choose 8}{16 \choose 8}(-2)^{2}\\ +{10 \choose 9}{18 \choose 9}(-2)^{1}\\ +{10 \choose 10}{20 \choose 10}(-2)^{0}\\ =252 $$

After we have calculated $\sigma(0),\ldots,\sigma(5)$ we can calculate the result $$\sum_{k=0}^{5}{10 \choose 2k}\sigma(k)\sigma(5-k)=13180608$$

Answer 6

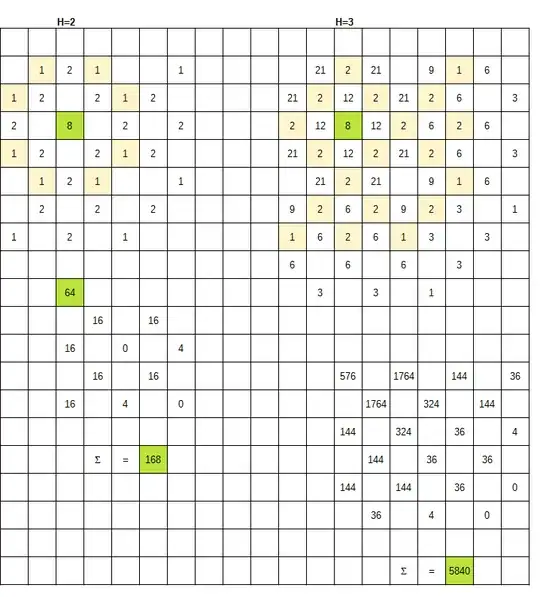
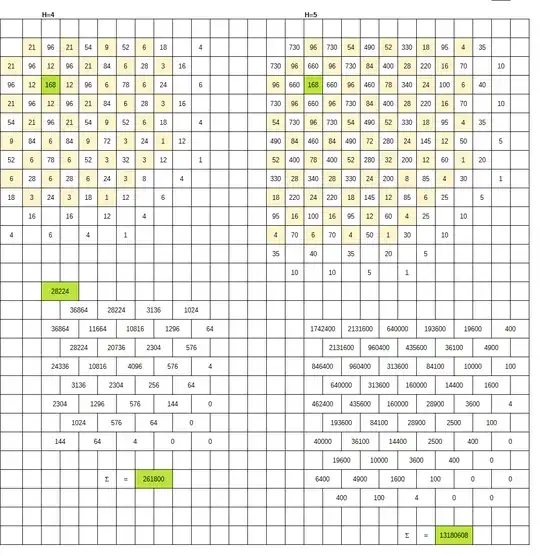
Easily to see that the length of the closed walk of the chess Knight is even. Assume it equals to $2H.$

Let us build the maps of the possible paths to the available positions of the figure for $H=1,2,3,4,5,$ using the previous (colored) map as the base for the next one.

The starting field in the all maps is colored to green. The map for $H=1$ is colored to light gold on the left picture and looks trivial (8 avaiilable fields with the single possible paths). This map is used on the all maps as a template for the summation of the paths quantities for the next map. Summation can be executed manually or via the electronic tables.

All calculations are executed only in one quadrant of the chessboard. The other fields are filled by the symmetry.

The total square sum counting is executed in the tables below. The green cell contains the square of the number in the green ceil of the map above. The white cells contains the squares of the cell of the map above with the factor 4. Since the higher map on the full chessboard are symmetric, then the total sum of the obtained map equals to the total square sum on the full chessboard.

See also the comments of miracle173.

Every Knight path consists of $H$ moves to the certain field and $H$ moves to returning, with the same quantity of the possible paths in the parts.

Therefore, the total sum of squares over the map for the halflength $H$ gives the quantity of possible closed paths of the length $2H,$ wherein this claim can be easily checked for $H=1,2,3.$

Thus, $$N_2 = 8,\quad N_4=168,\quad N_6 = 5840,\quad N_8 = 261800,\quad N_{10}=13180608.$$

Answer 7

Note: this answer doesn't have a complete solution to the 10-move case.

There's a few ways of thinking about this question. It seemed as though each avenue I went down hit a point of ever-increasing complexity as I tried to apply a method for the simplest case (2 moves, 4 moves etc) to the more generic n-move problem.

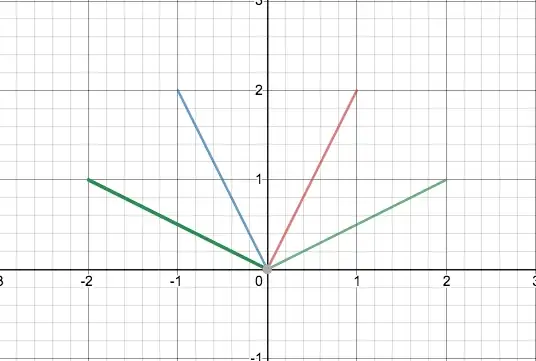
As I said in the question, there's 8 possible moves:

Each of these 4 and their equal and opposite (inverse) moves. The exclusion of the other four is deliberate and comes up later.

For the 4 move case:

The knight can either -

• Make one move, move back to origin, make another move, and move back to origin again, which has 8x8 = 64 permutations.
• Make one move, make the same move again, and then can only move back to the origin one way, which is by taking the inverse move twice. This has 8x1 = 8 permutations. EG take the red move twice in a row, then take the inverse of that twice again.
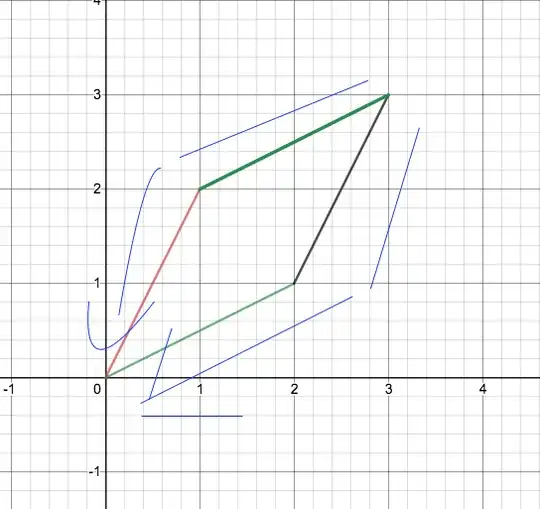
• Make one move, then take another move which is neither the same move or the inverse move, then take one of two ways back to the origin, which is to retrace the path (EG red move, green move, inverse of green, inverse of red) or take the way back to the origin which draws a parallelogram, illustrated below:

There are 8 first moves, 6 moves which are not the same move or the inverse, and then 2 ways to get back from there, so 8x6x2 = 96 permutations.

The sum is 64 + 8 + 96 = 168.

This is confirmed by rain1's link: oeis.org/A254129.

It is difficult to use this brute force approach for 6, 8 10 moves. As you can see in the link, the formulae found to compute A(n) are quite complicated.

A (slightly) more robust approach is as follows:

For the 10 move case, we take 5 moves from the 4 possible moves pictured (combinations with repeats). For each move that we pick, we need to take the inverse of that move in order to 'undo' the path we take. We're not placing the moves in order, we are simply taking some combination of 5 elements comprised of the 4 possible moves (EG red,red,red,blue,blue = blue,blue,red,red,red), and then assuming that we can only reverse this path by taking, for each move in the group of five, the inverse of that move. The combinations would be given by the terms in this expansion:

(x1 + x2 + x3 + x4) ^ 5.

Let's do this for the four move case. We first pick two moves from the possible 4:

• Take the same move twice. EG take red twice. We can do this 4 ways. For each group of 2 moves, the only way to undo this is to take the inverse moves. In this case, if we take 2 reds (the vector (1, 2)) then we must take the vector (-1, -2) twice to make a path back to the origin. So with those 4 moves, 2 of them are the vector (1,2) and two are the vector (-1, -2)and we calculate the permutations using the formula for permutations with identical elements:

  4! / (2! * 2!) = 6

  4 ways of doing this so 6*4 = 24.

• Take 2 distinct moves. EG red, green. We can do this 4C2 = 6 ways. Then we must take the two inverse moves, and our path is some permutation of the group [ red, green, inverse red, inverse green]. This has 4! permutations. So 6*4! = 144.

The sum is then 144 + 24 = 168.

If this approach is not clear, look at the expansion for (a + b + c + d)^2. If each letter is one of our 4 vectors, the terms in the expansion correspond to some combination of the vectors:

Expansion from Wolfram Alpha

a^2 + b^2 + c^2 + d^2 + 2 a b + 2 a c + 2 a d + 2 b c + 2 b d + 2 c d

Don't worry about the coefficients, they don't make strict sense in this case as we're adding the two inverse vectors to that combination. Just note that there are indeed 4 ways to take the same vector twice, and 6 ways to take 2 distinct vectors.

Now consider this approach for the 6-move case. Unfortunately I could not get the correct answer, though it was close, and I'm not sure where to go from here.

(a + b + c + d)^3:

• Take one vector 3 times: 4C1 = 4 ways of doing this, and then take the inverse vector 3 times. EG [red,red,red,inverse red,inverse red,inverse red,]. This combination makes 6!/( 3! * 3!) = 20 permutations. So 4 * 20 = 80 permutations using the same vector 3 times.

• Take one vector twice, and another vector once. This corresponds to terms of the form x^2 * y in the expansion. We would have 4 * 3 ways
  of doing this. EG [red,red,green]. Then include the inverse vectors
  to make the group of 6. This has 6! / ( 2! * 2!) permutations = 180. 180*12 = 2160.

• Take 3 distinct vectors. 4C3 * 6! = 2880.

Then the sum is 80 + 2160 + 2880 = 5120. According to rain1's link the answer is 5840, so I'm off by 720. I suspect this is because of the assumption that a vector can only be 'undone' by using its inverse vector and not some combination of the others. I think this holds for the 4 move case which is why it works.

In terms of where to go from here, I was hoping that the repliers to the original could help me out, because I can't seem to find a proper solution.