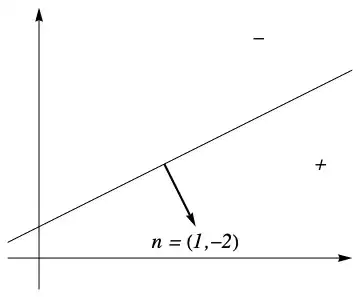
When we take distance from the line, we take
$$ d = \frac{ Ax_o + By_o + C}{ \sqrt{A^2 +B^2}}$$
usually with a modulus on top, now my question is if I evaluate this distance as negative what does it mean? Can I decide on which half-plane a point using this?
Expanding on the answer of @Andrew Chin, the sign says in which of the two half-planes (in which the line divides the whole plane) lays the point. If it is from the same side of the vector $(A,B)$ then the result is positive, otherwise negative. Sometime called oriented distance.
For example, for the line of equation $x-2y+1=0$ we have ${\bf n}=(A,B)=(1,-2)$ and the following graphic representation
The denominator is based on the magnitude of a vector and is always positive, but the numerator is based on the scalar product. Since the scalar product is based on the cosine ratio, if you find yourself a "negative distance", this just means that the angle between the vector being projected and the normal vector you have decided to use (i.e. $\vec n=(A,B)$ and not $\vec n=(-A, -B)$) is obtuse.
What I learnt is that $$d = \,\Large \mathbf{\pm} \normalsize\, \frac{ Ax_o + By_o + C}{ \sqrt{A^2 +B^2}}$$
To add to the answers, if we have a function $$ f(x,y) = Ax+By +C$$ Then we can understand that the family of parallel lines of the form $ Ax+By + C' = 0$ is level sets to the above. Taking the gradient, we find the normal of the line as:
$$ \nabla F = <A,B>$$
This is what @enoztib was talking about