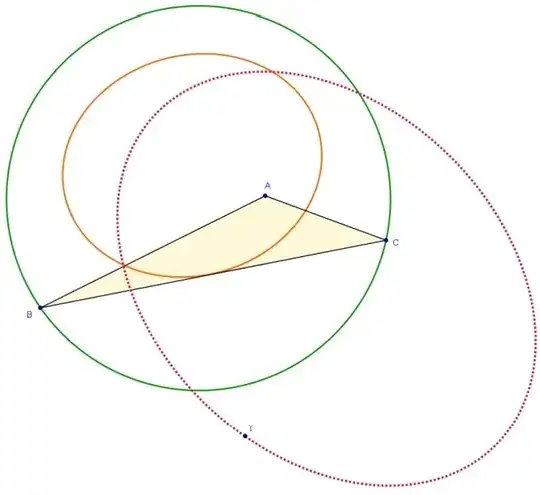
Given a point $A$, a circle $O$ and conic section $e$, if $BC$ is a moving chord of the circle $O$ tangent to $e$, then prove that
the locus of △$ABC$'s circumcenters $T$ is a conic section.
The question was posted in 纯几何吧 by TelvCohl and remained unsolved for many years but regrettably I cannot provide the link because the post was deleted by Baidu accidentally.
It seems that the locus related to circumcenter is often a conic section.Another example:
The directions of two sides of a triangle is fixed and the third side passes through a fixed point, then the locus of the circumcenter is a conic section.(The elementary geometry of conics.1883)
- 5,361
-
4Include your work in the question so that we may directly address your problem. – SarGe Jul 13 '20 at 16:28
-
5Where did the problem come from? – brainjam Jul 13 '20 at 18:41
-
I've noticed that If points $D,E,F,G,H$ on $e$ are mapped to points $D',E',F',G',H'$ the cross ratio (as in Section 2 of https://projecteuclid.org/download/pdf_1/euclid.chmm/1437147056) is preserved. If you could prove that, then the locus would be a conic section. – brainjam Jul 16 '20 at 17:01
-
1I couldn't track down the last remark in the 1883 reference, but a proof of that locus is in Hatton, pg 256, example 6 – brainjam Oct 24 '21 at 19:17
-
See equivalent problem Show that the locus of a point in this geometric construction is a conic and its answer. – brainjam May 02 '22 at 20:25
2 Answers
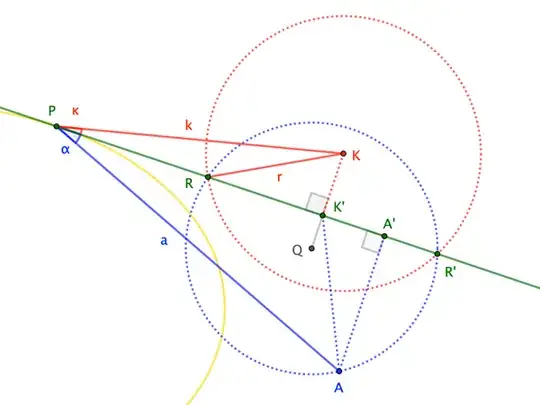
Here's something of a brute-force vector proof.
In the figure, $P$ is a point on our given conic, $\bigcirc K$ of radius $r$ is our given circle, and $A$ is our given point. The tangent line at $P$ meets $\bigcirc K$ at $R$ and $R'$, and the circumcenter of $\triangle ARR'$ is $Q$. Points $A'$ and $K'$ are the respective projections of $A$ and $K$ onto the tangent line. Finally, $a:=|PA|$, $k := |PK|$, and $\alpha$ and $\kappa$ are the (signed) angles made by the tangent line and the respective vectors $\overrightarrow{PA}$ and $\overrightarrow{PK}$.
First, a bit of geometry. Ignoring the conic, and concentrating how $\bigcirc K$ meets the tangent line and determines circumcenter $Q$, one can show that $|K'Q|$ is given by $$\begin{align} |K'Q| &= \frac{|AK'|^2 -|RK'|^2}{2|AA'|} \tag{1}\\[4pt] &= \frac{\left(a^2+|PK'|^2-2a|PK'|\cos\alpha\right)-\left(r^2-|KK'|^2\right)}{2a\sin\alpha} \tag{2}\\[4pt] &= \frac{a^2+k^2\cos^2\kappa-2ak\cos\alpha\cos\kappa-r^2+k^2\sin^2\kappa}{2a\sin\alpha} \tag{3}\\[4pt] &= \frac{a^2+k^2-2ak\cos\alpha\cos\kappa-r^2}{2a\sin\alpha} \tag{4} \\[4pt] &= \frac{a^2+k^2-2ak\cos(\alpha+\kappa)-2ak\sin\alpha\sin\kappa-r^2}{2a\sin\alpha} \tag{5}\\[4pt] &= \frac{|AK|^2-r^2-2ak\sin\alpha\sin\kappa}{2a\sin\alpha} \tag{6}\\[4pt] &= \frac{|AK|^2-r^2}{2a\sin\alpha}-k\sin\kappa \tag{7}\\[4pt] &= \frac{|AK|^2-r^2}{2a\sin\alpha}-|KK'| \tag{8} \\[4pt] \end{align}$$
Therefore, we can write, defining $s := |AK|$, $$Q = K + (P')^\perp (|KK'|+|K'Q|) = K + \frac{s^2-r^2}{2a\sin\alpha}\,(P')^\perp \tag{9}$$ where $(P')^\perp := (P'_y,-P'_x)$ is perpendicular to $P'$;that is, it's a unit normal to the conic. (We could take either normal. The calculation of $a\sin\alpha$ in $(12)$ ensures that $Q$ is properly offset from $K$.)
Now, to bring the conic back into consideration ... Let us suppose that $P$ lies on an origin-focused conic, with corresponding vertex on the positive $x$-axis, latus rectum $p$, and eccentricity $e$. Then $P$ is parameterized by $$P = \frac{p}{1+e\cos\theta}\;(\cos\theta,\sin\theta) \tag{10}$$ The unit tangent vector is then $$P' = \frac1{\sqrt{1+e^2+2e\cos\theta}} (\sin\theta, -(e + \cos\theta)) \tag{11}$$ We also have $$ a \sin\alpha = (P')^\perp\cdot(A-P) = \frac{p - A_x(e+\cos\theta) - A_y \sin\theta}{\sqrt{1 + e^2 + 2 e \cos\theta}} \tag{12} $$ Substituting into $(9)$ we find the locus point $(x,y)=Q$ parameterized as
$$(x,y) = K + \frac{s^2-r^2}{2(p - A_x(e+\cos\theta) - A_y \sin\theta)}(e+\cos\theta,\sin\theta) \tag{13}$$ Separating the components and clearing denominators gives equations that happen to constitute a linear system in $\cos\theta$ and $\sin\theta$; solving and substituting into $\cos^2\theta+\sin^2\theta=1$ gives a second-degree polynomial equation in $x$ and $y$ which necessarily represents a conic.
For completeness, the equation is as follows:
$$\begin{align} 0 &= 4 x^2 (p + A_x (1-e)) (p - A_x(1+e))\\ &+ 4 y^2 ( p^2 - A_y^2(1-e^2)) \\ &-8 x y\, A_y (ep+A_x(1-e^2)) \\ &+4 x(A_x (s^2-r^2+2A_x K_x+2A_y K_y) (1-e^2) + ep( s^2 - r^2 + 4 A_x K_x + 2 A_y K_y ) - 2 K_x p^2 ) \\ &+4y ( A_y ( s^2 - r^2 + 2 A_x K_x + 2 A_y K_y ) (1-e^2) + 2 ep A_y K_x - 2 p^2 K_y ) \\ &-(s^2 - r^2 + 2 A_x K_x + 2 A_y K_y)^2 (1 - e^2) - 4 e p K_x (s^2 - r^2 + 2 A_x K_x + 2 A_y K_y) + 4 p^2 (K_x^2 + K_y^2) \end{align} \tag{$\star$}$$
Defining $m^2=s^2-r^2+2(A_xK_x+A_yK_y)=|OA|^2+|OK|^2-r^2$, we can write this as
$$\begin{align} 0 &= 4 x^2 (p + A_x (1-e)) (p - A_x(1+e)) \\ &+ 4 y^2 ( p^2 - A_y^2(1-e^2)) \\ &-8 x y\, A_y (ep+A_x(1-e^2)) \\ &+4 x(A_x m^2 (1-e^2) + ep( m^2 +2A_xK_x) - 2 K_x p^2 ) \\ &+4y ( A_ym^2 (1-e^2) + 2 ep A_y K_x - 2 p^2 K_y ) \\ &-m^4 (1 - e^2)- 4 e p K_x m^2+ 4 p^2 |OK|^2 \end{align} \tag{$\star'$}$$
which isn't much of an improvement, but I don't think the equation is the important thing here.
The discriminant (ignoring a factor of $64p^2$) reduces to $|OA|^2 - (p - e A_x)^2$, which indicates that the nature of the resulting conic (ellipse, parabola, hyperbola) depends only upon $A$'s position relative to the focus.
- 83,939
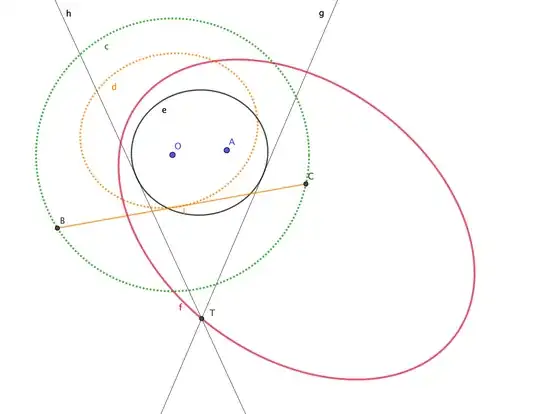
This an observation, not an answer, that is too long to put in a comment. It introduces a new conic, and runs the OP's construction in reverse. The diagram below is based on the the original diagram, and adds a given conic $e$ (in black) with foci $O$ and $A$ and major axis length $r$. The other given conic is $f$ (rose colored). The reverse construction will create the green circle and the orange conic.
For a point $T$ on $f$, construct its tangents to $e$. Reflect point $A$ in both tangents, producing points $B$ and $C$. (the tangents are the perpendicular bisectors in the original construction whose intersection is the circumcenter.) Then as $T$ moves on $f$, $B$ and $C$ run along the circle $c$, and the moving chord $BC$ traces an envelope of conic $c$ (orange).
Circle $c$ has center $O$ and radius $r$ and is the orthotomic circle of $e$ with respect to focus $A$. Which is basically the pedal curve of $e$ with respect to $A$, scaled up by 2. It's also known as the directrix circle of $e$.
All this said, it's not obvious that this observation will help getting the proof requested in the question.
- 9,172