How can we prove that a non-linear equation of motion for a classical scalar field satisfies causality?

Question

Let $\phi$ be a real-valued scalar field in $N$-dimensional spacetime with coordinates $(t,\vec x)$, and consder the equation of motion $$ (\partial_t^2-\nabla^2)\phi(t,\vec x)+V'\big(\phi(t,\vec x)\big)=0 \tag{1} $$ where $\nabla$ is the gradient with respect to the spatial coordinates $\vec x$, and where $V'$ is the derivative of a non-negative polynomial such that $V(\phi)=0$ if and only if $\phi=0$.

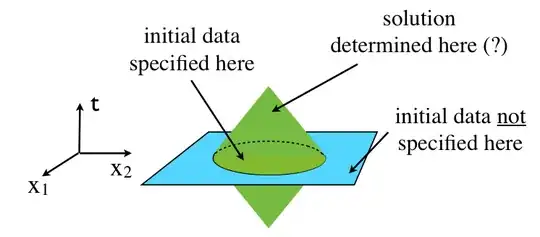
Suppose that smooth initial data ($\phi$ and $\partial_t\phi$) is spedified at $t=0$ for all $\vec x\in R$, where $R$ is some bounded region of space. Physics folklore says that this determines the solution everywhere in the causal completion of $(t=0,R)$, which consists of all points $(t,\vec x)$ that are outside the light-cones of all points $(t=0,\vec x\notin R)$ where the initial data was not specified. This is illustrated below:

If this folklore is true, then how can it be proven?

• I can prove it when the initial data is zero (posted below as a self-answer), and this implies the result for nonzero initial data when equation (1) is linear, but I don't know how to prove it when the initial data is nonzero in the nonlinear case.

• I've searched the online literature for keywords like hyperbolic PDEs, domain of dependence, and characteristics, among others, and I've learned a lot from this, but so far I haven't recognized anything that answers this question.

Answer 1

Here's a proof in a very special case, namely when the initial data is zero. I learned this appraoch based on a tip in a comment by Ninad Munshi, which led me to this answer by Willie Wong on Math Overflow, which includes a link to these lecture notes (pdf file) by Qian Wang.

Let $B(t)$ be the intersection of the causal completion of $(t=0,R)$ with the constant-time hyperplane at the specified time $t$. Define $$ \newcommand{\pl}{\partial} E(t)\equiv \int_{\vec x\in B(t)} \left( \frac{\dot\phi^2+(\nabla\phi)^2}{2}+V(\phi) \right). \tag{2} $$ The conditions on $V$ given in the question imply that this is nonnegative and that it is zero if and only if $\phi$ and its time-derivative $\dot\phi\equiv\pl_t\phi$ are both zero in $B(t)$ at the specified time. Consider $t>0$, so that $B(t)$ shrinks as $t$ increases, and take the time-derivative of (2) to get \begin{align*} \dot E &= \int_{\vec x\in B(t)} \Big( \ddot\phi\dot\phi+(\nabla\phi)\cdot(\nabla\dot\phi)+V'(\phi)\dot\phi \Big) \\ &\phantom{=} - \int_{\vec x\in \partial B(t)} \left( \frac{\dot\phi^2+(\nabla\phi)^2}{2}+V(\phi) \right) \\ &= \int_{\vec x\in B(t)} \Big( \ddot\phi-\nabla^2\phi+V'(\phi) \Big)\dot\phi \\ &\phantom{=} + \int_{\vec x\in B(t)} \nabla\cdot\big(\dot\phi\nabla\phi\big) \\ &\phantom{=} - \int_{\vec x\in \partial B(t)} \left( \frac{\dot\phi^2+(\nabla\phi)^2}{2}+V(\phi) \right). \end{align*} The second integral in the first equation comes from the $t$-dependence of the integration domain $B(t)$, and $\pl B(t)$ denotes the boundary of $B(t)$. If $\phi$ satisfies the equation of motion (1), then the first term in the second equation is zero. The second term in the second equation may be written as an integral over the boundary $\pl B(t)$, with unit normal $\vec n$. This gives \begin{align*} \dot E &= \int_{\vec x\in \pl B(t)} \vec n\cdot\big(\dot\phi\nabla\phi\big) \\ &\phantom{=} - \int_{\vec x\in \partial B(t)} \left( \frac{\dot\phi^2+(\nabla\phi)^2}{2}+V(\phi) \right) \\ &= - \int_{\vec x\in \partial B(t)} \left( \frac{\big(\vec n\dot\phi-\nabla\phi\big)^2}{2}+V(\phi) \right). \end{align*} This is nonpositive, so $E(t)$ must be a decreasing function of time for $t>0$. But $E(t)$ is nonnegative, so if it's zero initially, then it's zero for all $t>0$, because it cannot decrease any further.

This answers the question for the special case when the initial data is zero, which implicitly also answers the question with arbitrary initial data in the special case of a linear equation of motion (because then the difference of two solutions is another solution).