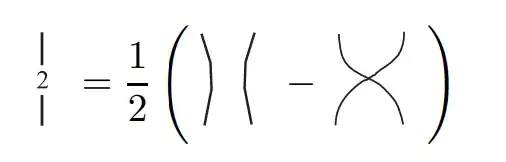In the paper here https://arxiv.org/pdf/gr-qc/9905020.pdf we see an introduction to Spin-networks of the original Penrose type i.e an undirected open graph whose edges have labels that are irreducible representations of SU(2).
In particular given a set of label 1 edges (that represent spin 1/2), here shown with no label, it is said that one can create higher label wires as follows:
Where $S_n$ is the space of permutations of n and $|\sigma|$ is the number of 'wire crossings' induced by said permutation. Looking at this it appears to be a projector from the Hilbert space $\otimes_n H^{ 2}$ to its anti-symmetric subspace - essentially a direct generalisation of how this
sends $H^{2}\otimes H^{2}$ to its anti-symmetric subspace.
My question is how does this gel with representation theory? Is it the case that any irreducible representation can somehow be seen in terms of an anti-symmetric projector on a tensor product space of Hilbert spaces acted on by an appropriate number of copies the fundamental rep of SU(2)?
Doubtless my relative weakness in representation theory is apparent. I'm approaching this problem due to some overlap with quantum computing so the more things are tied to concrete things like qubit basis', and fundamental SU(2) operations the more likely I will understand what is going on.