I have encountered an basic operation on a set of intervals which I think should have a common name and be in textbooks. Unfortunately, my searches have turned up empty.
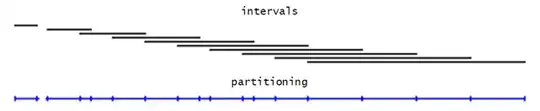
Imagine you have a set of intervals $I$. From this set, you want to calculate a partitioning $P$. Namely, you want to find the set of disjoint intervals which partitions $I$ into sub-intervals such that for each interval $p$ in $P$, all points contained in $p$ overlap with the same intervals in $I$.
The closest I’ve found which resembles this kind of operation is the “sectioned” operation of an R package called IntervalSurgeon.
Any help would be greatly appreciated! I’ve encountered this problem in the context of a master thesis about the analysis of timed systems. The context is that the intervals represent time ranges during which the system displays a certain behaviour while the partitions are time ranges for which you know that for all points of time inside that time range the systems displays the same behaviour .