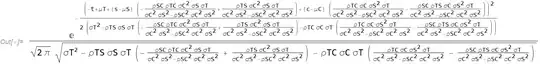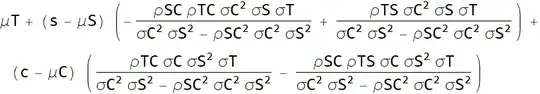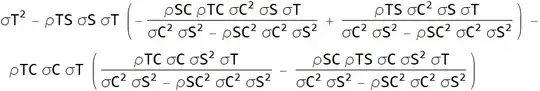Consider three non-independent normally distributed random variables $(T,S,C)$. I am interested in the distribution of $T$ conditional on $S=s$ and $C=c$.
I know that, for $\mu_T=\mu_S=\mu_C=0$ and $\sigma_T=\sigma_S=\sigma_C=1$, the conditional mean is given by
$E[T|S=s, C=c]=\beta_{TS;c} s+\beta_{TC;s} c$
where the betas are the regression coefficients: $\beta_{ij;k}=\frac{\rho_{ij}-\rho_{ik}\rho_{jk}}{\sqrt{1-\rho_{ik}^2}\sqrt{1-\rho_{jk}^2}}$
Is there a similar way to parameterise $Var[T|S=s, C=c]$?
NB. I'm not interested in a step-by-step derivation – I'd be equally happy with an expression derived from the symbolic integrals in Mathematica.