Equation of a "tilted" sphere

Asked May 31 '20 at 05:00

Active May 31 '20 at 05:24

Viewed 116 times

I'm looking for a simple two variable equation of a tilted sphere. I don't know what the precise terminology is, but it's similar to this.

Here is a picture: 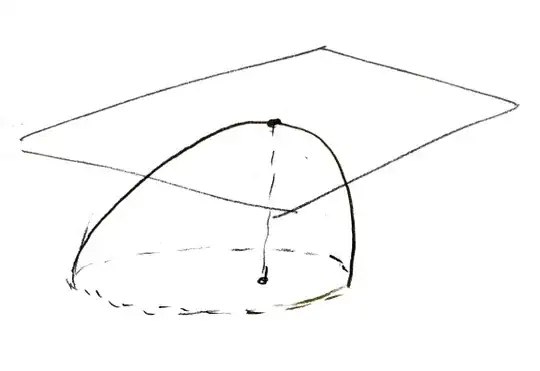The $f(x,y)=0$ at the dotted lines at the base of this shape. But this shape does not take on its maximum value when $x=0$ and $y=0$. Rather, it's sort of tilted to the side.

In particular, I need a continuously differentiable function $f : \mathbb{R}^2 \rightarrow \mathbb{R}$ such that $f(x,y)=0$ when $x^2+y^2=1$, but the point at which the tangent plane is parallel to the $xy$-plane is not at $(0,0).$ In other words, the top of the sphere is a little off center.

I'm having trouble constructing this. Whenever I introduce any "tilt/skew" to a single variable equation, I'm not sure how to make it satisfy the $f(x,y)=0$ when $x^2+y^2=1$ condition.

edited May 31 '20 at 05:24

asked May 31 '20 at 05:00

Snowball

1,159

Can you draw a "titled sphere"? This makes no sense. – David G. Stork May 31 '20 at 05:12
For one, I think it is meant to be "tilted;" other than that, I am not quite sure what the OP means. – Dylan C. Beck May 31 '20 at 05:13
What I imagine is an ellipsoid that is not centered at the origin and not in standard position. – Dylan C. Beck May 31 '20 at 05:15
I added a picture. I don't know what this sort of shape is called. – Snowball May 31 '20 at 05:24
I believe that this is an ellipsoid that is not centered at the origin and not in standard position. – Dylan C. Beck May 31 '20 at 05:35
It's not just moving an ellipsoid some units in one direction. I actually need the base to be fixed like a proper sphere would be, but just the top warped to the side, so that the tangent plane isn't touching the curve when x=0 and y=0. – Snowball May 31 '20 at 05:41

Equation of a "tilted" sphere

0 Answers0