My question is about parts c) and d) of this question:
Let $G = (V,E)$ be an oriented graph. For every pair of vertices $u,v \in V$, we write $u \leftrightarrow v $ iff there exists a path from $u$ to $v$ and a path from $v$ to $u$.
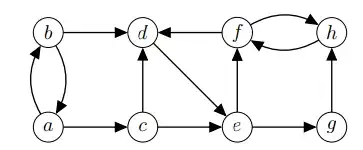
In a) I was asked to show that it is an equivalence relation. So I went on and explained reflexivity, symmetry and transitivity.
In b) I was asked to show the 'strongly connected' classes that have the relation $ \leftrightarrow $.
I have that $\{a,b\}$ and $\{f,h\}$ are strongly connected.... is this ok ?
Now in c). Let $P$ be a partition $P = \{V_1,V_2,...,V_k\}$ of the set of vertices $V$ of a graph $G$. We define the quotient graph as the graph $H$ of which the set of vertices is $P$ such that there exists an arc from $V_i$ to $V_j$ if $i \ne j $ and there exists an arc in $G$ from a vertex of $V_i$ to a vertex of $V_j$.
Calculate the quotient graph from the picture, for the partition given by the equivalence relation $\leftrightarrow$
I can't even understand it. Sorry if it's not clear, I have trouble translating it.
Where do I start with c)?
Also in d) I am asked to show that every quotient graph is acyclic...