Geometrical significance of r.h.s. of set of linear equations.

Question

Express $[3, 14]$ as a linear combination of $[3, 4]$ and $[1, -2]$.

$\begin{bmatrix} 3&4\\ 1&-2\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\14\end{bmatrix}\implies \begin{bmatrix} 3&4\\ 3&-6\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\42\end{bmatrix}\implies \begin{bmatrix} 3&4\\ 0&-10\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\39\end{bmatrix}\implies \begin{bmatrix} 3&4\\ 0&-1\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\3.9\end{bmatrix}$

$\implies \begin{bmatrix} 3&0\\ 0&-1\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}18.6\\3.9\end{bmatrix}\implies \begin{bmatrix} 1&0\\ 0&-1\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}6.2\\3.9\end{bmatrix}$

Also, the values of $a,b$ are unique to the set of linear equations, so the solution means: $a = 6.2, b= -3.9$.

I want to extend this question to see the geometrical significance of the rhs.

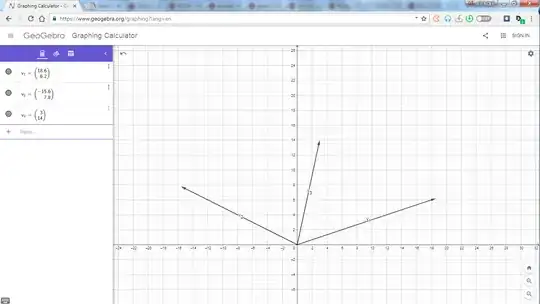
So, the column vectors are: $v_1=a\begin{bmatrix} 3\\ 1\\ \end{bmatrix}=\begin{bmatrix} 18.6\\ 6.2\\ \end{bmatrix}$, $v_2=b\begin{bmatrix} 4\\ -2\\ \end{bmatrix}=\begin{bmatrix} -15.6\\ 7.8\\ \end{bmatrix}$.

The original set of equations have two column vectors on left, and a r.h.s.

So, the r.h.s. of the original set of linear equations should have explicit representation in terms of $v_1, v_2$, as shown in the graphical representation below. Seemingly, it forms the diagonal of the parallelogram formed by two vectors $v_1, v_2$.

But, is there an algebraic approach to show the same; as such an approach can help to prove easily the relationship.

---

Edit:

The parallelogram law of vector addition can be used here to check the same.

Here $v_3 = v_1 + v_2$, so the formula would lead to :
$v_3^2 = v_1^2 + v_2^2 - 2v_1.v_2.cos\theta,$ where $\theta$ is the angle between $v_1$ and $v_2$.

It is found by taking sum of two angles- $\alpha, \beta$, as shown here (also, the previous page); which are found as follows:

(i) $\alpha$: angle made by $v_1$ with positive -$x$ axis.
It is given by $\tan^{-1}(\alpha) = \frac 13\implies \alpha = 18.41^o$.
(ii) $\beta$: clockwise angle made by $v_2$ with negative -$x$ axis.
So, will ignore the negative value of the fraction $-0.5$. It is given by $\beta = \tan^{-1}(0.5)\implies \beta = 26.57^o$

So, $\theta= \alpha+\beta = 18.41^o+26.57^o = 44.98^o$.

So, putting the values in the parallelogram vector law, get:

$v_3^2 = v_1^2 + v_2^2 - 2v_1.v_2.cos(44.98^o)$

Need to get the two sides match

$205 = 384.4 + 304.2 - 2(19.606)(17.44)(0.707) $

$205 = 688.6 - 2(19.606)(17.44)(0.707) $

$205 = 688.6 - (19.606)(17.44)(1.414) $

$205 = 688.6 - 483.48$

$205 = 205.12$

---

Edit 2 This is in answer to the comment by @gen-zreadytoperish, which seems to imply that the vectors on the l.h.s. given should also be taken as column vectors rather than as row vectors.
However, this is only possible when column vectors are taken from a system of equations with l.h.s. & r.h.s. So, it is a notation or convention.
My approach (earlier) was based on taking individual vectors with each component defining a dimension. My approach can, unlike the latter approach, take vectors as representing a point in space; but as stated earlier it is notation to use the latter one.

By this modification, we get : $\begin{bmatrix} 3&1\\ 4&-2\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\14\end{bmatrix}$

So, $\begin{bmatrix} 3&1\\ 2&-1\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\7\end{bmatrix}\implies \begin{bmatrix} 3&1\\ 5&0\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}3\\10\end{bmatrix}\implies \begin{bmatrix} 15&5\\ 15&0\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}15\\30\end{bmatrix}$$\implies \begin{bmatrix} 0&5\\ 1&0\\ \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}-15\\2\end{bmatrix} \implies a=2, 5b = -15\implies a=2, b = -3$

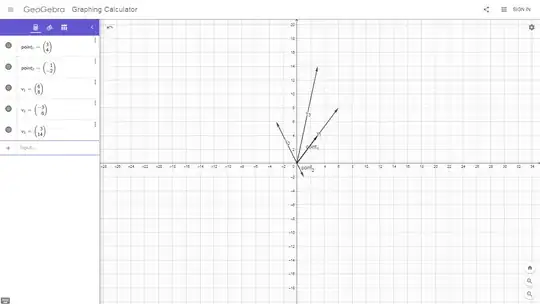
So, the column vectors are given by:

$v_1=a\begin{bmatrix} 3\\ 4\\ \end{bmatrix}=\begin{bmatrix} 6\\ 8\\ \end{bmatrix}$, $v_2=b\begin{bmatrix} 1\\ -2\\ \end{bmatrix}=\begin{bmatrix} -3\\ 6\\ \end{bmatrix}$.

The original set of equations have two column vectors on left, and a r.h.s.

So, the r.h.s. of the original set of linear equations should have explicit representation in terms of $v_1, v_2$, as shown in the graphical representation below. It forms the diagonal of the parallelogram (shown in image as $v_3$) formed by two vectors $v_1$, $v_2$.

Now need to prove by algebraic approach the relationship of the rhs vector as the diagonal of the parallelogram formed by $v_1, v_2$.

The parallelogram law of vector addition can be used here to check the same.

Here $v_3 = v_1 + v_2$, so the formula would lead to :
$v_3^2 = v_1^2 + v_2^2 - 2v_1.v_2.cos\theta,$ where $\theta$ is the angle between $v_1$ and $v_2$.

It is found by taking sum of two angles- $\alpha, \beta$, as shown above in Edit , found as follows:

(i) $\alpha$: angle made by $v_1$ with positive -$x$ axis.
It is given by $\tan^{-1}(\alpha) = \frac 43\implies \alpha = 53.123^o$.
(ii) $\beta$: clockwise angle made by $v_2$ with negative -$x$ axis.
So, will ignore the negative value of $-2$. It is given by $\beta = \tan^{-1}(2)\implies \beta = 63.43^o$

So, $\theta= \alpha+\beta = 53.123^o+63.43^o = 116.53^o$.

So, putting the values in the parallelogram vector law, get:

$v_3^2 = v_1^2 + v_2^2 - 2v_1.v_2.cos(116.53^o)$

Need to get the two sides match

$205 = 100(=6^2+8^2) + 45(=(-3)^2+(6)^2) - 2(10)(6.708)(-0.447025) $

$205 = 145 + (8.94)(6.708) $

$205 = 145 + 59.969 $

$205 = 204.969 $

---

As each set of two linear equations has a unique set of values possible for $(a,b)$. So, there is only one solution possible for each set of linear equations, as two linear equations can only intersect at a unique point. As have taken up two different sets of two equations, so got two separate solutions.
It can be seen that in both the set of two equations, the rhs vector : $v_3= \begin{bmatrix}3\\14\end{bmatrix}$ is forming diagonal of the two vectors $a.v_1, b.v_2$ in both cases, and satisfies the relation of $v_3 = a.v_1+b.v_2$.

---

Edit 3:

A useful site is: https://ximera.osu.edu/la/LinearAlgebra/VEC-M-0040/main.

Also, my first comment here is wrong in specifying the post (https://math.stackexchange.com/a/1960990/424260); as the post supports the second approach. Confused how it happened.

Answer 1

First regarding problem formulation:

You want to find $a$ and $b$ such that

$$a[3,4] + b[1,-2]=[3,14]$$

That is $$3a+b=3$$ $$4a-2b=14$$

We can write them in matrix form:

$$\begin{bmatrix} 3 & 1 \\4 & -2\end{bmatrix}\begin{bmatrix} a \\ b\end{bmatrix}=\begin{bmatrix} 3 \\ 14\end{bmatrix}\tag{1}$$

That is why you should put them in column rather than row.

Note that we have $$\begin{bmatrix} 3 & 1 \\4 & -2\end{bmatrix}\begin{bmatrix} a \\ b\end{bmatrix}=a\begin{bmatrix} 3 \\ 4\end{bmatrix} + b \begin{bmatrix} 1 \\ -2\end{bmatrix}$$

Alternatively, you can view them as $$\begin{bmatrix} a & b\end{bmatrix}\begin{bmatrix} 3 & 4 \\ 1 & -2\end{bmatrix}=\begin{bmatrix} 3 & 14 \end{bmatrix}$$

---

Now, regarding how to solve $(1)$, some of the ways include:

• perform Gaussian elimination
• solve the system of linear equations by substitution
• pre-multiply matrix inverse on both sides.

---

The solution is unique since the matrix is non-singular.

---

It seems that you are verifying the length of the vector by using cosine rule.

We indeed have $$205=100+45 -2(10)\cdot \sqrt{45}\cos(\arctan\left(\frac43\right)+ \arctan(2))$$

but as you round off numbers, you should be expecting that you are sacrificing some precision.

Note that $\beta = \tan^{-1}(2)$ and not $\tan^{-1}(-2)$ or you will get an obtuse angle.