17

On page 159 of "A Comprehensive Introduction To Differential Geometry Vol.1" by Spivak has written:

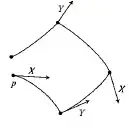
We thus see that the bracket $[X,Y]$ measures, in some sense, the extent to which the integral curves of $X$ and $Y$ can be used to form the "coordinate lines" of a coordinate system. If $X$ and $Y$ are two vector fields in a neighborhood of p, then for sufficiently small $h$ we can

(1) follow the integral curve of $X$ through $p$ for time $h$ ;

(2) starting from that point, follow the integral curve of $Y$ for time $h$;

(3) then follow the integral curve of $X$ backwards for time $h$ ;

(4) then follow the integral curve of $Y$ backwards for time $h$.

enter image description here

Question:

Before reading this book I thought that $\mathcal{L}_{X}Y=[X,Y]$ calculates changes of $Y$ along Integral curve of $X$.But in this Figure, the integral curves of both vector fields are used. I'm confused. Can someone help me?

Thanks.

glS
  • 7,963
Sepideh Bakhoda
  • 6,004
  • 1
    I think this is equivalent to the theorem: $[X,Y]=0 \iff$ the commutator of flows $\Phi_X^t \Phi_Y^s,\Phi_X^{-t}, \Phi_Y^{-s}$ is a closed loop. Right now I wouldn't know how to prove it, though... – A.P. Apr 14 '13 at 09:35
  • Maybe this question helps:http://math.stackexchange.com/questions/132897/geometric-intuition-behind-the-lie-bracket-of-vector-fields?rq=1 – gofvonx Oct 20 '13 at 17:31

2 Answers2

1

Maybe you confused $\mathcal L_X Y$ with $\mathcal L_X f$ where $X,Y$ are vector fields and $f$ is a smooth function?

The Lie derivative $\mathcal L_X f$ of a smooth function is defined by $\mathcal L_X f(x) = df(x)(X(x))$ for $x$ a point on our manifold, which in coordinates is given by $\dfrac{\partial f}{\partial x^i}(x)X^i(x)$ (using the summation convention). We can interpret $\mathcal L_X f$ as the directional derivative in the direction of the vector field $X.$

On the other hand, $\mathcal L_X Y$ is defined to be that vector field $Z$ satisfying $\mathcal L_Z f = \mathcal L_X\mathcal L_Y f-\mathcal L_Y\mathcal L_X f$ for all smooth functions $f.$ Namely, taking the directional derivative of any smooth function in the direction of $\mathcal L_X Y$ is equivalent to computing the difference between iterated directional derivatives in the $Y$ direction and $X$ direction. This can be interpreted in terms of flows by what you've written.

Andrew
  • 11,557
0

Well, you first idea about the Lie derivative is correct, too. Another characterization is $$(\mathcal{L}_X Y)_p f = \left. \frac{\mathrm{d}}{\mathrm{d}t} \right|_{t=0} (d_{\Phi(p,t)} \Phi(\cdot,-t)) Y_{\Phi(p,t)} f,$$ where $\Phi$ is the flow of $X$. So you follow the flow of $X$, evaluate $Y$ there and transport it back to the starting point by the differential of $\Phi$. The curve defined by this procedure lives in the tangent space to $p$ and its derivative is the Lie derivative of $Y$ with respect to $X$ at the point $p$. So it does measure the change of $Y$ along the integral curve of $X$.

I don't have a good explanation why those two ideas give the same object, though.

Thomas
  • 1,991
  • 9
  • 14