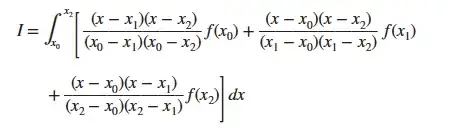3

I am reading how Simpson's Rule works for numerical integration. So I understand that given the two endpoints $x_0$ and $x_2$, and one intermediate point $x_1$, we can connect these points to make a parabolic function as an approximation to the original function which we want to integrate.

The book then proceeds to give the following formula, which I do not understand.

enter image description here

Where did the coefficients of $f(x_0), f(x_1), f(x_2)$ come from?

Rodrigo de Azevedo
  • 23,223
cgo
  • 1,970

2 Answers2

1

The interpolating polynomial can be written as \begin{align*} p_2(x)= &\sum_{i=0}^2 L_i(x) f(x_i)=\sum_{i=0}^2 \frac{\prod_{j \ne i}(x-x_j)}{\prod_{j \ne i}(x_i-x_j)} f(x_i)\\ =& \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0)+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}f(x_1)+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2) \end{align*}

Simpson's formula just uses, as you mention, the approximation $$ \int_{x_0}^{x_2} f(x)dx \approx \int_{x_0}^{x_2} p_2(x) dx. $$

Note: this works because $L_i(x_j) = \delta_{ij}$.

PierreCarre
  • 23,092
  • 1
  • 20
  • 36
  • Another approximate formula for $\int_a^b f(x)dx$ is $\frac {(b-a)}{18}( 5f(x_{-1})+8f(x_0)+5f(x_1))$ where $x_0=(a+b)/2$ and $x_{\pm 1}=x_0\pm (|b-a|/2)\sqrt {3/5},$ which is exact when $f$ is a polynomial of degree $5$ or less. – DanielWainfleet Mar 24 '20 at 07:06
0

Let

$$F(x)={(x-x_1)(x-x_2)\over(x_0-x_1)(x_0-x_2)}f(x_0)+{(x-x_0)(x-x_2)\over(x_1-x_0)(x_1-x_2)}f(x_1)+{(x-x_0)(x-x_1)\over(x_2-x_0)(x_2-x_1)}f(x_2)$$

Note that

$$\begin{align} F(x_0)&={(x_0-x_1)(x_0-x_2)\over(x_0-x_1)(x_0-x_2)}f(x_0)+{(x_0-x_0)(x_0-x_2)\over(x_1-x_0)(x_1-x_2)}f(x_1)+{(x_0-x_0)(x_0-x_1)\over(x_2-x_0)(x_2-x_1)}f(x_2)\\ &=1\cdot f(x_0)+0\cdot f(x_1)+0\cdot f(x_2)\\ &=f(x_0) \end{align}$$

Likewise, we find that

$$F(x_1)=0\cdot f(x_0)+1\cdot f(x_1)+0\cdot f(x_2)=f(x_1)$$ and $$F(x_2)=0\cdot f(x_0)+0\cdot f(x_1)+1\cdot f(x_2)=f(x_2)$$

In other words, the coefficients of $f(x_0)$, $f(x_1)$, $f(x_2)$ are chosen so that each becomes appropriately $1$ or $0$ when we plug in $x=x_0$, $x_1$, and $x_2$; the numerator in each coefficient is what makes it $0$ or not; the denominator is what makes the coefficient equal to $1$ when it's nonzero.

A remark on terminology: Each of the "coefficients" here is a quadratic in $x$, so the function $F(x)$ is a quadratic polynomial, $F(x)=Ax^2+Bx+C$, where the "coefficients" $A$, $B$, $C$ are functions of $x_0$, $x_1$, $x_2$. Don't confuse one set of coefficients with the other!

Barry Cipra
  • 81,321