10

On page 12 of "Lectures On Ricci Flow" by Peter Topping is written:

In two dimensions, we know that the Ricci curvature can be written in terms of the Gauss curvature $K$ as $Ric(g) = Kg$. Working directly from the equation $\frac{\partial g}{\partial t}=-2Ric(g) $, we then see that regions in which $K < 0$ tend to expand, and regions where $K > 0$ tend to shrink.

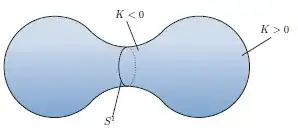
Can anyone solve the Ricci flow PDE in this case and show regions in which $K < 0$ tend to expand, and regions where $K > 0$ tend to shrink?

thanks

Parcly Taxel
  • 105,904
Sepideh Bakhoda
  • 6,004

2 Answers2

11

Substituting $Ric=Kg$ into the Ricci flow equation we get $\dot g = -2Kg$, where $\dot g$ is the time derivative of $g$. Since $K$ is a scalar, this equation simply means that every component of $g$ satisfies the same equation (considering $g$ as a matrix): $\dot g_{ik}=Kg_{ik}$, where $i,k=1,2$. Hence, without loss of generality assuming that $g$ is a diagonal matrix, if $K<0$ then $\dot g_{ii}>0$, which means that the length of a vector, say $v$, will grow for a short time at least (more precisely, the time derivative of the length will be positive).

timur
  • 17,004
  • @ timur: OK, this means that $g_{ik}=a_{ik} e^{-2Kt}$, where $i,k=1,2$ and $a_{ik}$ is components of initial metric. Then $R_{ik}=Ka_{ik}e^{-2Kt}$. Since weyl tensor is vanished in two dimensions, the curvature is determined completely by Ricci curvature. Now if $K<0$ and $t \to \infty$ ,then, dependent on $a_{ik}>0$ Or $a_{ik}<0$, $R_{ik}\to -\infty$ Or $+\infty$. But this result seems false because this shape under Ricci flow becomes a circle. I'm confused.... – Sepideh Bakhoda Apr 11 '13 at 18:29
  • 3
    @Bakhoda: Note that the solution is not so simple because $K$ depends on $g$. – timur Apr 11 '13 at 18:38
  • @ timur: thanks. – Sepideh Bakhoda Apr 11 '13 at 18:44
1

Have a look at the paper An example of neckpinching for Ricci flow on $S^{n+1}$ by S. Angenent and D. Knopf.

According to the review by Peng Lu,

The authors construct a class of initial metrics on $S^{n+1}$ so that the corresponding Ricci flow solutions develop neck pinching at singular time $T$. The singularity is of Type I in the sense of Hamilton, and the length of the neck, where the curvature tensor $\vert Rm\vert\sim(T-t)^{-1}$, is bounded from below by $c\sqrt{(T-t)\cdot\vert\log(T-t)\vert}$ for some constant $c>0$.

Jocko
  • 21