2

I am trying to simulate a Brownian Bridge starting at $0$ and finishing at $\alpha$ at some time $T$ in an Excel spreadsheet. However I am not sure the behaviour I am getting is to be expected, namely the simulated Brownian Bridge's trajectory becomes approximately linear after a certain point.

I base my Brownian Bridge on the representation found in this question: $$B_t = \alpha \frac{t}{T}+\left(1-\frac{t}{T}\right)\int_{0}^T \dfrac{dW_s}{1-\frac{s}{T}}$$ My simulation scheme is as follows, with $n$ the total number of simulation steps and $\delta=1/n$, where $i$ represents a simulation step: $$\begin{align} & N_i \leftarrow Z \sim \mathcal{N}(0,1) \\ & w_i \leftarrow \delta^{1/2}N_i \\ & B_i \leftarrow \alpha i\delta+(1-i\delta)\sum_{j\leq i}(1-j\delta)^{-1}w_j \end{align}$$ I display below one such simulation of the Brownian Motion $W$ and the Brownian Bridge $B$ (anchored at $0$ both at beginning and end):

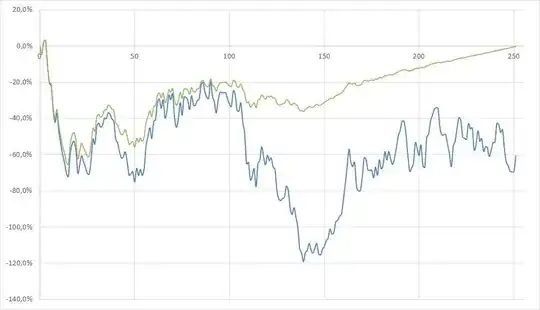
Clearly the Bridge behaves less and less like a random quantity as we approach the terminal time. This does not seem right to me. Is there something wrong with my simulation procedure? What is going on here?

Morris Fletcher
  • 651
  • 1
    FYI : you get the same result (a Brownian bridge from $(0,0)$ to $(T,\alpha)$) by considering $(B_t - (t/T) (B_{T}-\alpha))_{0 \le t \le T}$ – Olivier Mar 09 '20 at 20:31
  • Intuitively, I would just simulate the Brownian motion $W(t)$ from $0$ to $T$ and then plot $W(t)-t(W(T)-W(0))/T$. Namely, just obtain the usual Brownian trajectory and then remove the random drift that you obtain. – Quillo Mar 29 '22 at 10:15

0 Answers0