The question is now also published in MathOverflow (here).
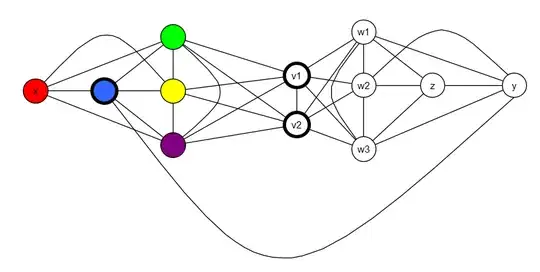
I'm trying to solve a problem about connectivity of entangled vertices in a graph.
Two vertices $u, v$ of a finite graph $G(V, E)$ are said to be entangled if for any proper coloring $c:V(G)\rightarrow\mathbb{N}$ with $\chi(G)$ colors we have $c(u) = c(v)$, that is, they must have the same color.
What I'm trying to prove is that, given two entangled vertices $u, v\in V(G)$, there is $w\in V(G)$ (possibly equal to $v$) also entangled with $u$ so that there is a set of size $\chi(G)-1$ of disjoint paths from $u$ to $w$.
EDIT: The proof cited below was incorrect, as shown by the accepted answer.
I was able to prove, using the vertex-connectivity version of Menger's theorem and induction, that the previous statement is true if $v$ is the only vertex in $G$ entangled with $u$, so I've been trying to show that if there is not a set of size $\chi(G)-1$ of disjoint paths from $u$ to $v$ (considering $u$ and $v$ entangled), there is still a vertex in $G-v$ entangled with $u$, but without success.
Another idea I had was showing that the minimal (in the number of edges) subgraph of $G$ for which there is still a vertex entangled with $u$, has exactly one vertex entangled with $u$.
I would appreciate some help with this subject.