5

I am looking for alternative of sigmoid curves going through $(0,0)$, whose parameters can be sensed by eyeballing the function graph. As an example, consider this curve:

$$f(x) = {{a x ^ b} \over 1 + a x ^ b}$$

Where $ a, b $ are meaningless parameters without any straightforward interpretation. However, we can write the curve equation in such a way that both parameters will be meaningful. Imagine new parameters $c, d$ such that:

$$\begin{cases} f (c) = 0.1 \\ f (d) = 0.9 \end{cases}$$

Then expressing the curve with parameters a, b defined as follows, that is by parameters c, d, does the job.

$$\displaystyle{a}={9}\cdot{d}^{{-{b}}}$$

$$\displaystyle{b}=\frac{{-{4}\cdot \log{{\left({3}\right)}}}}{ \log{{\left(\frac{c}{{d}}\right)}}}$$

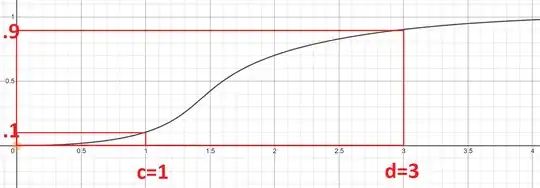
So looking at the example below, we can easily guess the values of parameters c, d. The function is in 10% and 90% value in approximately $x=1$ (parameter c) and $x=3$ (parameter d). Job done.

graph

https://www.desmos.com/calculator/fmalvakguo

Why I ask for alternatives? The curve equation lacks "symmetry." I do not ask for exact symmetry but what I mean is that the function above $f(d)=0.9$ approaches asymptote of 1 very slowly. While below $f(c)=0.1$ the function gets to zero quite quickly.

Przemyslaw Remin
  • 51
  • It is unclear what kind of symmetry you are looking for. You say that the asymptote of 1 is approached slowly, compared to the value $0$. But the interval $(0,c)$ is bounded wheras $(d,\infty)$ is unbounded so I don't know what you expect. Do you want any specific convergence rates? – Hyperplane Feb 17 '20 at 21:47
  • 1
    @Hyperplane I would be very happy if different s-curves are presented here, which can be expressed using 10% and 90% parameters. In this question, symmetry is only a flavor, not a focus. The Weibull curve presented in the answer looks relatively symmetrical compared to the function I brought in the question. I would not measure that symmetry. – Przemyslaw Remin Feb 18 '20 at 10:00

2 Answers2

12

enter image description herejust putting this out there as a potential answer and hopefully encouraging others to do the same ... how about the Weibull "stretched exponential" function $$f(x)=1-e^{-{\left(\frac{x}{a}\right)}^{b}}$$ where $b>2$

depending on the value of $b$ (pictured in graph are $b=3,4,5$), the symmetry can vary quite a bit, while $a$ sets the scale for $x$-axis

one can reexpress the $a$ and $b$ parameters as a function of $c$ and $d$ as provided in problem definition $$f(c)=0.1$$ and $$f(d)=0.9$$

and then, for instance, $$b=\frac{\ln \left(-\ln 0.1 \right) - \ln \left(-\ln 0.9 \right)}{\ln d - \ln c}$$ with $$a=c \left( -\ln 0.9 \right)^{-1/b}$$

phdmba7of12
  • 1,068
1

$f(x)=\frac{1}{1+9^{\frac{(c-x)}{s}}}$ statisfies your criteria, is perfectly symmetric, and has many of the pretty properties of the logistic function due to being directly derived from it. The function reaches $0.5$ at $c$ and reaches $.1$ or $.9$ at $c\pm s$. If you want your $s$ to describe the location of WLOG $.03$, set the base of your exponent to $\frac{1-.03}{.03}$.

EDIT: The above function does not have the point $(0,0)$. We can take $g(x)=(f(x)-.5)*(1+f(0))+.5$ to include $(0,0)$ and $(2c,1)$.

Erez Abrams
  • 167
  • Can you please rewrite it with parameters c, d as described in the problem definition? (0,0) is required function property, thus I would be grateful if you could write full equation for your g(x, c, d). – Przemyslaw Remin Feb 21 '20 at 08:57
  • Thanks for this function. I find it very useful. Your second form, however, does also not have the point (0,0) although it comes closer – Horst Lemke Apr 22 '22 at 12:38