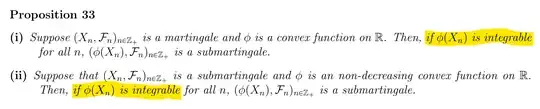0

I'm reading a proposition about Martingale in my lecture note:

enter image description here

From the definition of martingale, I get $X_n$ is integrable. From this thread, I get the composition of a convex function with an integrable function is integrable. As such, $\phi(X_n)$ is automatically integrable.

Is the condition if $\phi\left(X_{n}\right)$ is integrable redundant?

Thank you so much ;)

Akira
  • 18,439

2 Answers2

2

If $X$ is integrable it does not follow that $X^{2}$ is. And $x \to x^{2}$ is convex. In the link you provided they are talking about Riemann integrability and boundedness of the function plays an important role. But an intergable random variable need not be bounded.

Kavi Rama Murthy
  • 359,332
  • The text says non-decreasing (and $x^2$ is non-decreasing somewhere, but not everywhere). However, the same reasoning works for $e^x$. –  Feb 08 '20 at 11:48
  • 1
    @Gae.S. Thanks for the comment. There is no mention of monotonicity in the first part. For the second part we can take $e^{x}$ if monotonicity is insisted on the whole line. – Kavi Rama Murthy Feb 08 '20 at 11:56
1

Of course not. Take for example $(\Omega ,\mathcal F,\mathbb P)=((0,1),\mathcal B,m)$ where $m$ is the Lebesgue measure and $\mathcal B$ being the $\sigma -$algebra of Borel set of $(0,1)$. Let $$X_n(\omega )=\omega,\quad \omega \in \Omega ,$$ for all $n$ and define $\varphi :(0,\infty )\to \mathbb R$ by $$\varphi (x)=\frac{1}{x}.$$ Then $\varphi $ is convex, but $\varphi (X_n)$ is never integrable.

Surb
  • 57,262
  • 11
  • 68
  • 119