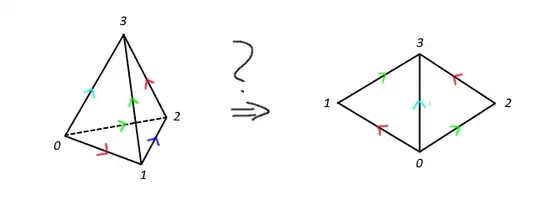
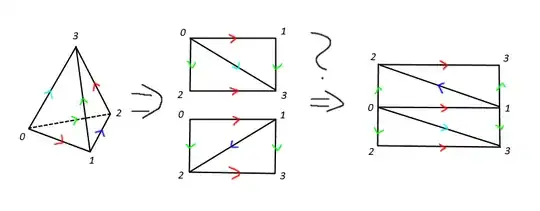
I'm trying to show that the $3$-simplex with the edge identifications $[v_0, v_1] \sim [v_2, v_3]$ and $[v_0, v_2] \sim [v_1, v_3]$ deformation retracts onto the torus. I have a couple of potential solutions, but I'm not sure why/if they are correct.
The first one is inspired by this solution to a similar problem. This involves collapsing the face $[v_0, v_1, v_2]$ by identifying the edge $[v_1, v_2]$ with $[v_1, v_0] + [v_0, v_2]$, giving the "usual" scheme for a torus, as shown in the figure below. However, I'm not quite sure why this is allowed. What exactly happens with the edge $[v_1, v_2]$, shown in dark blue?
The other solution is to try to cut the $3$-simplex and then glue it together again in a way that shows that it is a torus, as inspired by this solution. I'm not really sure how to get this to work though. I always end up with weird things like shown in the figure below. What am I doing wrong?
Thanks in advance!