Why Markov matrices always have 1 as an eigenvalue

Question

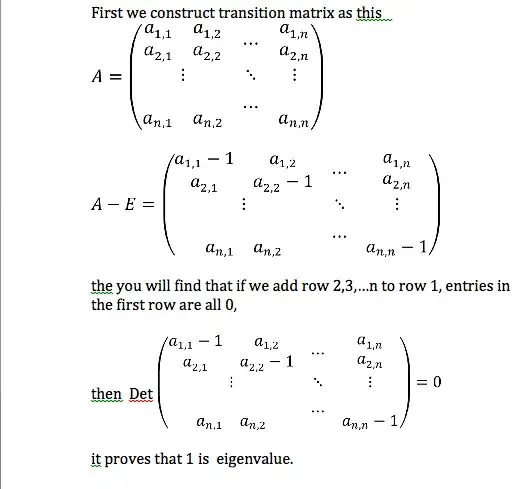
Also called stochastic matrix. Let

• $A=[a_{ij}]$ - matrix over $\mathbb{R}$

• $0\le a_{ij} \le 1 \forall i,j$

• $\sum_{j}a_{ij}=1 \forall i$

i.e the sum along each column of $A$ is 1. I want to show $A$ has an eigenvalue of 1. The way I've seen this done is that $A^T$ clearly has an eigenvalue of 1, and the eigenvalues of $A^T$ are the same as those of $A$. This proof, however, uses determinants, matrix transposes, and the characteristic polynomial of a matrix; none of which are particularly intuitive concepts. Does anyone have an intuitive, alternate proof (or sketch of proof)?

My goal is to intuitively understand why, if $A$ defines transition probabilities of some Markov-chain, then $A$ has an eigenvalue of 1. I'm studying Google's PageRank algorithm.

Answer 1

I just encounter the same problem as you do, here is my solution.

I upload my solution by picture

Answer 2

My intuition is that since $A$ describes a transition from some vector that encodes probability distribution to another vector that also encodes probability distribution, $A$ is not allowed to scale up or scale down the vector along the same direction, because otherwise that vector will no longer have all its entries add up to $1$ and it would no longer be a probability distribution.

In other words, suppose $A$ is a markov matrix, and $v$ is a vector that represents some probability distribution. This means that all the entries in $v$ have to add up to one.

Now let $v'= vA$. If $v$ were an eigenvector, that means that $v' = \lambda v$. Since $v'$ is also a probability distribution, all its entries must also add up to $1$, and this can only happen if $\lambda = 1$.

Answer 3

Suppose that $M$ has a left eigenvector, $u$, with eigenvalue $\lambda$: $$ u^T(M-I\lambda)=0\tag{1} $$ Let $\{v_j\}_{j=1}^n$ be the columns of $M-I\lambda$. Equation $(1)$ says that for all $j$, $u\perp v_j$.

Being $n+1$ vectors in $\mathbb{R}^n$, $u$ and $\{v_j\}_{j=1}^n$ must be linearly dependent. That is, there are $a$ and $\{b_j\}_{j=1}^n$, not all $0$, so that $$ au+\sum_{j=1}^nb_jv_j=0\tag{2} $$ If we take the dot product of $u$ with $(2)$, we get $$ \|u\|^2a+\sum_{j=1}^n0\,b_j=0\tag{3} $$ That is, $a=0$. Thus, $(2)$ becomes $$ \sum_{j=1}^nb_jv_j=0\tag{4} $$ where not all $b_j$ are $0$. $(4)$ can be rewritten as $$ M\begin{bmatrix}b_1\\b_2\\b_3\\\vdots\\b_n\end{bmatrix} =\lambda\begin{bmatrix}b_1\\b_2\\b_3\\\vdots\\b_n\end{bmatrix}\tag{5} $$ Therefore, $M$ has a right eigenvector with eigenvalue $\lambda$.

Answer 4

For a Markov matrix A, we know the j-th diagonal element of $(A-I)$ can be expressed as $-\sum^n_{i \neq j} a_{ji}$.

It may not be too obvious to see that $det(A-I)=0$, while it is easier to prove $det((A-I)^T)=0$. This is because, for $(A-I)^T x =0$, we have non-zero solution $x=(1,1,\cdots,1)$, indicating $(A-I)^T$ is singular. For square matrix $(A-I)$, we have $det(A-I)=det((A-I)^T)=0$, hence, we know $1$ is an eigenvalue of Markov matrix A.

Answer 5

Let $A$ be a stochastic matrix as you stated in your question. Let $\mathbf{1}$ be a column vector of all $1$s. Then the $j$th component of $A1$ is the sum of the $j$th row of $A$. This gives $A1 = 1$. Thus $\lambda = 1$ is an eigenvalue corresponding to the eigenvector 1.

Also when you try to diagonalize a stochastic matrix that all rows sum to 1 the characteristic polynomial will factor out $(\lambda -1)$ no matter what the rest of the polynomial will be.

Answer 6

When we calculate eigen values and eigen vectors: Given an eigenvalue Y, and eigenvector associated with Y is a non zero vector x such that: (A-YI)x=0

Now in markov chain a steady state vector ( when effect multiplying or any kind of linear transformation on prob state matrix yield same vector) :

qp=q where p is prob state transition matrix this means Y = 1 as an eigen vector of P' which also means

There is an unique probability vector q which is an eigenvector associated with eigenvalue 1.