3

Recently I was studying the quasi-inverse. Before I studied the quasi-inverse, I revisited the inverse and the left-right inverse.

inverse function:

Let $f : X → Y$, $g : Y → X$ is inverse of $f$, if only if, $f∘g = id_{Y}$ and $g∘f = id_{X}$.

It is easy to understand.

right-inverse function:

Let $f : X → Y$, $g : Y → X$ is right-inverse of $f$ (or section of $f$ ), if only if , $f∘g = id_{Y}$.

It means that $f$ must be surjective and $g$ must be injective. It is also very intuitive.

Now I start to study quasi-inverse:

One thing I have to explain here is that the "quasi-inverse" does not seem to be a precise terminology and I can't find any information about quasi-inverse in wikipedia or nlab. (I study it because the form of "quasi-inverse" appears in many branches of mathematics, e.g. in category theory, adjoint functors needs to satisfy triangular identity. Although they are completely different, they are similar in form)

Here, I use the definition of quasi-inverse from https://planetmath.org/QuasiinverseOfAFunction

Let f:X→Y be a function from sets X to Y. A quasi-inverse g of f is a function g such that

  1. g:Z→X where ran⁡(f)⊆Z⊆Y, and

  2. f∘g∘f=f, where ∘ denotes functional composition operation.

Note that ran⁡(f) is the range of f.

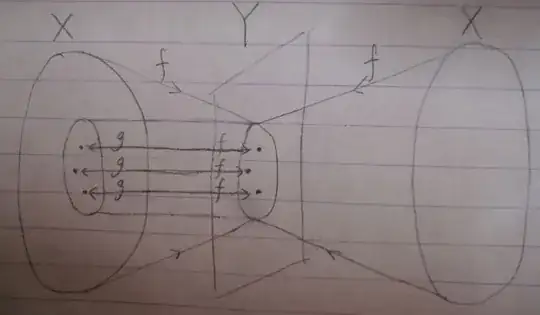
In order to understand this formula intuitively, I drew the following diagram

enter image description here

This formula seems to tell us that

A function $g$ is a quasi-inverse of a function $f$, if the restriction of $g$ to $ran(f)$ is the right-inverse of $f$, i.e.

$f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$

Note: $j_{S}$ denote identity function on $S$.

My first question is, is this conclusion correct? i.e.

$f ∘ g ∘ j_{ran(f)} = j_{ran(f)} \Leftrightarrow f∘g∘f=f $

If this conclusion is correct, how to prove it?

It is easy to prove $\Rightarrow$, but how to prove the opposite?

If this conclusion is wrong, anyone can give me an example which satisfies $f∘g∘f=f$ but not satisfies $f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$?

I may have missed some key things...

The second question is, if I have $f∘g∘f=f$ and $g∘f∘g=g$, is there any interesting conclusion? e.g. it can be concluded that f and g are bijection?

Very thanks.

PS: The reference of https://planetmath.org/QuasiinverseOfAFunction mentioned a book "Probabilistic Metric Spaces". In this book, the author mentioned another definition of quasi-inverse, which is stronger than the two quasi-inverses here, but it is another topic.

Community
  • 1
chansey
  • 595
  • 1
    There are other names for this, which makes it a bit more difficult to search for. See, for instance, https://en.wikipedia.org/wiki/Generalized_inverse. – Arthur Jan 01 '20 at 14:10
  • 1
    @Arthur Thanks, the generalized inverse is a new name for me. It seems to focus only on matrix transformation. Is there any reference which explains this kind of quasi-inverse using function and functional composition? – chansey Jan 01 '20 at 14:30
  • 1
    If $fgf=f$, then if $f(x)=y\in \operatorname{im} f$, we have $fgy = fgfx = fx=y$. Thus $fgf=f$ implies $fgj=j$, where $j$ is the inclusion of the image in $Y$. – jgon Jan 02 '20 at 01:24

1 Answers1

2

After some research, I have been able to answer my own question.

1. Prove $f∘g∘f=f ⇒ f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$

Proof by contradiction:

if $f ∘ g ∘ j_{ran(f)} ≠ j_{ran(f)}$, then must $∃y∈ran(f)$, such that $f ∘ g ∘ j_{ran(f)}(y) ≠ j_{ran(f)}(y)$, i.e. $f(g(y)) ≠ y$.

Since $y∈ran(f)$ and $f$ is a function, $y$ must have a (at least one) preimage element $x1$ such that $f(x1) = y$.

We already know $f∘g∘f=f$, apply $x1$ on both sides of the equation, we get

$f(g(f(x1))) = f(x1)$

$f(g(y)) = y$

But $f(g(y)) ≠ y$, which is a contradiction.

Thus $f∘g∘f=f ⇒ f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$ holds.

It is easy to see that $f∘g∘f=f ⇔ f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$

2. If I have $f∘g∘f=f$ and $g∘f∘g=g$, is there any interesting conclusion?

The interesting conclusion is $ran(g) = ran(g∘j_{ran(f)})$.

Prove as follows:

Note that ($f∘g∘f=f$ and $g∘f∘g=g) ⇔ (f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$ and $g ∘ f ∘ j_{ran(g)} = j_{ran(g)}$)

Since $ran(g)$ and $ran(g∘j_{ran(f)})$ are sets, so we must prove two-side inclusion.

(1) $ran(g∘j_{ran(f)}) ⊆ ran(g)$

It holds automatically.

(2) $ran(g) ⊆ ran(g∘j_{ran(f)})$

Proof by contradiction:

If (2) doesn't hold, then must $∃x∈ran(g)$ such that $x ∉ ran(g∘j_{ran(f)})$.

We already know $g ∘ f ∘ j_{ran(g)} = j_{ran(g)}$, apply $x$ on both sides of the equation, we get

$g(f(j_{ran(g)}(x))) = x$

Since $f(j_{ran(g)}(x))∈ran(f)$, $g(f(j_{ran(g)}(x)))∈ran(g∘j_{ran(f)})$.

But $g(f(j_{ran(g)}(x))) = x$, $x ∉ ran(g∘j_{ran(f)})$, which is a contradiction.

Thus $ran(g) ⊆ ran(g∘j_{ran(f)})$

Combining (1) and (2) yields $ran(g) = ran(g∘j_{ran(f)})$.

It is easy to see that $ran(f) = ran(f∘j_{ran(g)})$.

To summarize:

There are two kinds of definition of quasi-inverse, one is from https://planetmath.org/QuasiinverseOfAFunction, the other is from the book "Probabilistic Metric Spaces".

The former definition is to say that:

A function g is a quasi-inverse of a function f, if $f∘g∘f=f$.

This is equivalent to say that:

A function $g$ is a quasi-inverse of a function $f$, if the restriction of $g$ to $ran(f)$ is the right-inverse of $f$.

So this $g$ should actually be called "quasi-right-inverse" of $f$.

The latter definition is to say that:

A function $g$ is a quasi-inverse of a function $f$, if $f ∘ g ∘ j_{ran(f)} = j_{ran(f)}$ and $ran(g) = ran(g∘j_{ran(f)})$.

This is equivalent to say that:

$f∘g∘f=f$ and $g∘f∘g=g$

So this $g$ is the true quasi-inverse of $f$.

PS: The above proofs use natural language and may not be precise. If I'm wrong, please correct me, thanks. (BTW, in the book "Probabilistic Metric Spaces", the author mentioned a kind of function algebra. At first, I wanted to use this language to prove, but it was very difficult.)

chansey
  • 595