Problem statement
Can we find all monic polynomials of degree $n\in\mathbb N$ with real nonzero roots $x_1,\dots,x_n$ , such that their coefficients are equal to their roots multiplied by some real nonzero constant $\alpha$?
$$ P_n(x)=\prod_{i=1}^n(x-x_i)=x^n+\sum_{i=1}^n(\alpha x_{n-i+1})x^{n-i} $$
Roots of such polynomials can be obtained by simply dividing the coefficients by $\alpha$.
When $\alpha=1$, the problem is equivalent to "roots = coefficients" problem asked on MSE. That case is now resolved, and has exactly $4$ such polynomials, which is summarized in this answer.
I'm interested in expressing all solutions for given $n$, in terms of $\alpha\ne 0$ in general.
To solve this, we can apply Vieta's formulas to express the coefficients using the roots. This gives a nonlinear system of $n$ equalities. Is it possible to obtain general solutions to such systems?
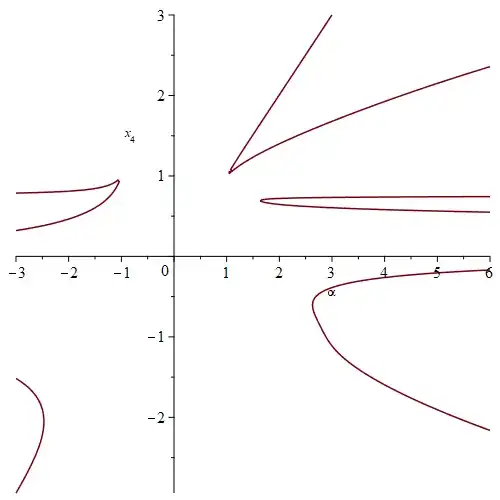
Remark: Golden ratio $\phi=\frac{1+\sqrt5}{2}=1.6180\dots$ appears in $n=3$ case, a nice coincidence.
Solutions for $(n\le 3)$
It is given that $x_1,\dots,x_n,\alpha\ne 0$ are nonzero and real.
- $(n=1)$: The first case is trivial and can only have solutions if $\alpha=-1$. $$P_1(x)=(x-x_1)=x+\alpha x_1\iff -x_1=\alpha x_1\iff (\alpha=-1,x_1\in\mathbb R\setminus\{0\})$$
$(n=2):$ The second case is also trivial to solve. $$\begin{align} &P_2(x)= x^2+(-x_1-x_2)x+x_1x_2 = x^2+\alpha x_2 x^1 + \alpha x_1 \\ \iff &\begin{cases}x_1x_2&=\alpha x_1 \\ -x_1-x_2&=\alpha x_2\end{cases}\\\iff &(x_2=\alpha,x_1=-\alpha(\alpha+1),\alpha\in\mathbb R\setminus\{-1,0\})\end{align}$$ Implying all such quadratic polynomials are of form: $$P_2(x)=x^2+\alpha^2x-\alpha^2(\alpha+1),\alpha\in\mathbb R\setminus\{-1,0\}$$ Whose roots are simply $x_2=\alpha$ and $x_1=-\alpha(\alpha+1)$.
$(n=3):$ This case requires solving the system (given by Vieta's formulas): $$\begin{cases} -x_1x_2x_3&=\alpha x_1\\ x_1x_2+x_2x_3+x_3x_1&=\alpha x_2\\ -x_1-x_2-x_3&=\alpha x_3 \end{cases}$$ I have used a CAS (Specifically, Mathematica's
Reduce[]) to solve this (where the raw output can be seen here). We have obtained:
If $\alpha=-1$, then the only solution is trivial: $(x_1=-1, x_2=1, x_3=1)$.
Otherwise, to write down the nontrivial solutions, we need to define helper polynomials: $$\begin{align}g_1(t)&=\alpha ^2-2 \alpha ^4-\alpha ^5+(-\alpha ^2+\alpha ^3+2 \alpha ^4) t+(2 \alpha +\alpha ^2-\alpha ^3) t^2-\alpha t^3+t^4\\g_2(t)&=-\alpha(\alpha+1)+t x_1+t^2\\h(t)&=144-92 t-243 t^2+20 t^3\end{align}$$ Define $\mathcal R(f,m)$ as the $m$-th smallest (real) root of $f=f(t)$ polynomial.
If $x_1$ is the smallest root of $g_1(t)$, that is if $x_1=\mathcal R(g_1,1)$, then: $$ x_2=\begin{cases} \mathcal R(g_2,1), & \text{if }\alpha\ge\mathcal R(h,2) \\ \mathcal R(g_2,2), & \text{if }\alpha\le\mathcal R(h,1) \\ \text{Isn't a solution}, & \text{else} \end{cases}$$ If $x_1$ is the $2$nd smallest root of $g_1(t)$, that is if $x_1=\mathcal R(g_1,2)$, then: $$ x_2=\begin{cases} \mathcal R(g_2,1), & \begin{cases}\text{ if }\alpha\lt-1,&\text{ and }\alpha\ne-\phi \\ \text{ or }\alpha\gt\mathcal R(h,2),&\text{ and }\alpha\ne\phi^{-1}\end{cases}\\ \mathcal R(g_2,2), & \text{if }-1\lt\alpha\lt\mathcal R(h,1) \\ \text{Isn't a solution}, & \text{else} \end{cases}$$ If $\alpha=\mathcal R(h,3)$ and $x_1=R(g_1,3)$ then $x_2=\mathcal R(g_2,2)$. Else, if $\alpha\gt\mathcal R(h,3)$ and either $x_1=\mathcal R(g_1,3)$ or $x_1=\mathcal R(g_1,4)$, then $x_2=\mathcal R(g_2,2)$. Otherwise, we do not have a solution.
Finally, the $x_3$ is always given as: $x_3=\frac{-\alpha}{x_2}$.
Notice how $x_1,x_2$ are given as specific roots of some $g_1,g_2$. This is the simplest way I could find to write down the nontrivial $(n=3)$ solutions.
Solving $(n\ge 4)$
Can we solve these nonlinear systems for $x_1,\dots,x_n$ in terms of $\alpha$, in general?
The systems are obtained from Vieta's formulas for given $n\in\mathbb N$.
To solve a system we can first solve the part of the system given by Vieta's formulas for coefficients next to $x^{n-1},\dots,x^1$ to obtain roots $x_1,\dots,x_{n-1}$ in terms of $\alpha$.
Looking at $(n=3)$, I suspect the roots $x_1,\dots,x_{n-1}$ would need to be expressed using specific roots $\mathcal R(g,m_g)$ of some $g_1,g_2,g_3,\dots$ where the cases of $m_g$ and $\alpha$ would depend on roots of some $h_1,h_2,\dots$
The root $x_n$ can be then obtained as (from $x^0$ equation of the system given by Vieta):
$$ x_n=\frac{(-1)^n\alpha}{\prod_{j=2}^{n-1}x_j} $$
The problem is solving this for larger $n$ and obtaining $g_1,g_2,g_3,\dots$ and $h_1,h_2,\dots$
Is there a general method to solve such a nonlinear system of $n$ equalities?
What is known about systems of $n$ nonlinear equations that involve expressions equal to or similar to Vieta's Formulas for degree $n$ polynomial?
If this is too hard, ways to solve one or more of the next cases $n=4,5,\dots$ will be useful.
Alternatively, perhaps we could try to solve for necessary forms of roots $x_1,\dots,x_n$. We ignore finding specific conditions on $\alpha$, and prioritize finding sets of values that the roots can take, which will be represented by roots of some helper polynomials $g_j^{(n)}(t)$ where $j\in\{1,2,\dots,n\}$ is a helper polynomial for $x_j$.
The following helper polynomials (patterns for "closed forms") of $x_1,x_2$, were obtained with Mathematica (Only for $n\le 4$ so far.):
Form of $x_1\text{?}$
For $n=1$, $x_1\in\mathbb R$ and $\alpha=-1$. Otherwise, $\alpha\in\mathbb R$ and $x_1$ takes values as roots of some $g_1^{(n)}(t)$.
For $n=2$, the $x_1$ must be the root of the polynomial $g_1^{(2)}(t)=$
$$ t^1\\ +(\alpha+\alpha ^2)t^0 $$
For $n=3$, the $x_1$ must be one of the roots of the polynomial $g_1^{(3)}(t)=$
$$ t^4\\ +(-\alpha )t^3\\ +(2 \alpha +\alpha ^2-\alpha ^3) t^2\\ +(-\alpha ^2+\alpha ^3+2 \alpha ^4) t^1\\ +(\alpha ^2-2 \alpha ^4-\alpha ^5)t^0 $$
For $n=4$, the $x_1$ must be one of the real roots of the polynomial $g_1^{(4)}(t)=$
$$t^{18}\\ +(-2 \alpha )t^{17}\\ +(-2 \alpha )t^{16}\\ +\left(2 \alpha ^4+5 \alpha ^2+6 \alpha \right) t^{15}\\ +\left(-5 \alpha ^5+\alpha ^4-7 \alpha ^2\right) t^{14}\\ +\left(2 \alpha ^6-5 \alpha ^5-9 \alpha ^4-10 \alpha ^3-10 \alpha ^2\right) t^{13}\\ +\left(\alpha ^8+14 \alpha ^6+22 \alpha ^5+14 \alpha ^4+21 \alpha ^3+15 \alpha ^2\right) t^{12}\\ +\left(-3 \alpha ^9+4 \alpha ^8+6 \alpha ^7-9 \alpha ^6+2 \alpha ^5+3 \alpha ^4-8 \alpha ^3\right) t^{11}\\ +\left(3 \alpha ^{10}-\alpha ^9-19 \alpha ^8-38 \alpha ^7-52 \alpha ^6-48 \alpha ^5-39 \alpha ^4-20 \alpha ^3\right) t^{10}\\ +\left(-\alpha ^{11}-2 \alpha ^{10}-13 \alpha ^9-13 \alpha ^8+29 \alpha ^7+62 \alpha ^6+50 \alpha ^5+38 \alpha ^4+20 \alpha ^3\right) t^9\\ +\left(-2 \alpha ^{11}+10 \alpha ^{10}+71 \alpha ^9+118 \alpha ^8+78 \alpha ^7+30 \alpha ^6+9 \alpha ^5-2 \alpha ^4\right) t^8\\ +\left(2 \alpha ^{12}+15 \alpha ^{11}+15 \alpha ^{10}-48 \alpha ^9-135 \alpha ^8-146 \alpha ^7-101 \alpha ^6-60 \alpha ^5-20 \alpha ^4\right) t^7\\ +\left(-4 \alpha ^{12}-42 \alpha ^{11}-108 \alpha ^{10}-116 \alpha ^9-23 \alpha ^8+65 \alpha ^7+65 \alpha ^6+38 \alpha ^5+15 \alpha ^4\right) t^6\\ +\left(-5 \alpha ^{13}-14 \alpha ^{12}+12 \alpha ^{11}+109 \alpha ^{10}+196 \alpha ^9+160 \alpha ^8+61 \alpha ^7+11 \alpha ^6+2 \alpha ^5\right) t^5\\ +\left(\alpha ^{14}+12 \alpha ^{13}+52 \alpha ^{12}+94 \alpha ^{11}+46 \alpha ^{10}-74 \alpha ^9-128 \alpha ^8-94 \alpha ^7-43 \alpha ^6-10 \alpha ^5\right) t^4\\ +\left(3 \alpha ^{14}+\alpha ^{13}-40 \alpha ^{12}-120 \alpha ^{11}-145 \alpha ^{10}-63 \alpha ^9+23 \alpha ^8+38 \alpha ^7+21 \alpha ^6+6 \alpha ^5\right) t^3\\ +\left(-\alpha ^{15}-10 \alpha ^{14}-25 \alpha ^{13}-19 \alpha ^{12}+34 \alpha ^{11}+95 \alpha ^{10}+87 \alpha ^9+33 \alpha ^8+5 \alpha ^7+\alpha ^6\right) t^2\\ +\left(\alpha ^{15}+7 \alpha ^{14}+19 \alpha ^{13}+30 \alpha ^{12}+20 \alpha ^{11}-19 \alpha ^{10}-46 \alpha ^9-34 \alpha ^8-12 \alpha ^7-2 \alpha ^6\right) t^1\\ +(-\alpha ^{13}-6 \alpha ^{12}-11 \alpha ^{11}-5 \alpha ^{10}+7 \alpha ^9+10 \alpha ^8+5 \alpha ^7+\alpha ^6) t^0$$
For $n=5$, the $x_1$ must be one of the real roots of the polynomial:
$$ g_1^{(5)}(t)=\text{?} $$
Is it possible to find these polynomials for $n\ge 5$?
Is it possible to find a closed form for $g_1^{(n)}(t)$ for all $n\in\mathbb N$?
Form of $x_2\text{?}$
For $n=2$, the $x_2$ must be the root of the polynomial $g_2^{(2)}(t)=$
$$ t^1\\ +(-\alpha)t^0 $$
For $n=3$, the $x_2$ must be one of the roots of the polynomial $g_2^{(3)}(t)=$
$$ t^2\\ +(x_1) t^1 \\ +(-\alpha^2-\alpha)t^0 $$
For $n=4$, the $x_2$ must be one of the real roots of the polynomial $g_2^{(4)}(t)=$
$$ t^6\\ + (-\alpha +2 x_{1}-\alpha x_{1})t^5\\ + (-2 \alpha x_{1}+\alpha ^2 x_{1}+3 x_{1}^2-\alpha x_{1}^2)t^4\\ + (-2 \alpha -\alpha ^2+\alpha ^3-2 \alpha x_{1}^2+\alpha ^2 x_{1}^2+2 x_{1}^3-\alpha x_{1}^3)t^3\\ + (\alpha ^2-\alpha ^3-2 \alpha ^4-2 \alpha x_{1}+2 \alpha ^3 x_{1}-\alpha x_{1}^3+x_{1}^4)t^2\\ + (\alpha ^3+2 \alpha ^4+\alpha ^5+\alpha ^2 x_{1}-\alpha ^3 x_{1}-2 \alpha ^4 x_{1}-2 \alpha x_{1}^2-\alpha ^2 x_{1}^2+\alpha ^3 x_{1}^2)t^1\\ +(\alpha ^2+\alpha ^3)t^0 $$
For $n=5$, the $x_2$ must be one of the real roots of the polynomial:
$$ g_2^{(5)}(t)=\text{?} $$
Is it possible to find these polynomials for $n\ge 5$?
Is it possible to find a closed form for $g_2^{(n)}(t)$ for all $n\in\mathbb N$?
Closed form for $x_i,i\ge 3\text{?}$
I do not have sufficient data for $n\ge 5$, hence I can't discuss these cases.
Answering "closed form" questions for $x_1,x_2$ alone looks hard enough.
At this point, any additional insights into the problem are welcome.