5

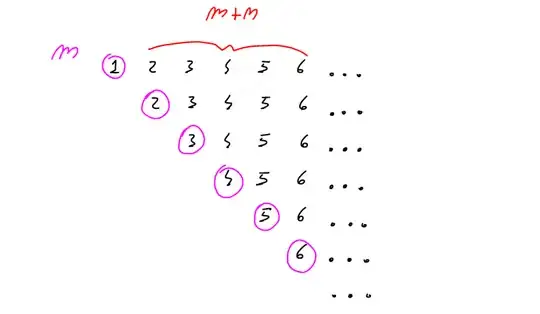
Check whether $$\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\frac{1}{\left(m+n\right)^2}$$ converges or NOT?

My Try:- $\sum _{m=1}^{\infty }\lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(m+n\right)^2}=\lim_{j\to \infty}\sum _{m=1}^{j }\lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(m+n\right)^2}=\lim_{j\to \infty}(\lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(1+n\right)^2}+ \lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(2+n\right)^2}+ \lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(3+n\right)^2}+...\lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(j+n\right)^2})\ge \lim_{j\to \infty}(j\lim_{i\to \infty} \sum _{n=1}^{i}\frac{1}{\left(j+n\right)^2})$

How do I complete the conclusion?

Truth_searcher
  • 171
  • 5

4 Answers4

9

If the series were convergent, we would have

$$\sum_{m=1}^\infty \sum_{n=1}^\infty \frac{1}{(m+n)^2} \geqslant\sum_{m=1}^\infty \sum_{n=1}^m \frac{1}{(m+n)^2} \geqslant \sum_{m=1}^\infty \sum_{n=1}^m \frac{1}{(2m)^2} \geqslant \sum_{m=1}^\infty \frac{1}{4m},$$

leading to a contradiction since the harmonic series on the right is divergent.

RRL
  • 92,835
  • 7
  • 70
  • 142
  • I did like this please see, $$ \sum_{m=1}^\infty \sum_{n=1}^\infty \frac{1}{(m+n)^2} = \sum_{m=1}^\infty \left( \zeta(2) - \sum_{n=1}^m \frac{1}{n^2} \right) $$ Can I say "it diverges"? –  Sep 06 '23 at 17:46
3

By double counting we have

$$\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\frac{1}{\left(m+n\right)^2}=\sum_{k=2}^\infty \frac{k-1}{k^2}=\sum_{k=2}^\infty \frac{1}{k}-\sum_{k=2}^\infty \frac{1}{k^2}$$

therefore the given series diverges.

enter image description here

user
  • 162,563
  • Not a bad idea -- but does that mean every double series diverges just because the inner series converges? If $\sum_{n \geqslant 1} a_{mn} = A_m \geqslant 0$ converges we can't conclude from this that $\sum_{m \geqslant 1} A_m$ diverges. – RRL Nov 07 '19 at 18:21
  • You are absolutely right! I need to revise that! Thanks – user Nov 07 '19 at 18:25
  • @RRL In this way it should be better! – user Nov 07 '19 at 19:18
2

Fix $k$;

$k=m+n$; $k \ge 3$;

there are $(k-1)$ elements with $m+n=k$;

$m=k-1, n=1$; $m=k-2, n=2$;

$m=1, n=k-1;$

$\sum_n\sum_m \dfrac{1}{(m+n)^2}= \sum_{k=3}^{\infty} \dfrac{(k-1)}{k^2}$

Divergent.

Peter Szilas
  • 21,123
2

From $$\frac1{(m+n)^2}=-\int_0^1 x^{m+n-1}\ln xdx$$

it follows that

$$S=\sum_{m=1}^\infty\sum_{n=1}^\infty\frac1{(m+n)^2}=-\int_0^1\frac{\ln x}{x}\left(\sum_{m=1}^\infty x^m\right)\left(\sum_{n=1}^\infty x^n\right)dx=-\int_0^1\frac{x\ln x}{(1-x)^2}dx\\=-\int_0^1\ln x\left(\frac1{(1-x)^2}-\frac1{1-x}\right)dx$$

Clearly, the first integral is divergent so $S$ diverges,

$$\int_0^1\frac{\ln x}{(1-x)^2}dx=\sum_{n=1}^\infty n \int_0^1 x^{n-1}\ln xdx=-\sum_{n=1}^\infty \frac{n}{n^2}\\=-\lim_{k\to \infty}\sum_{n=1}^k \frac1n=-\lim_{k\to \infty}H_k=-\infty$$

where $H_k$ is the harmonic number.

Ali Olaikhan
  • 27,891