0

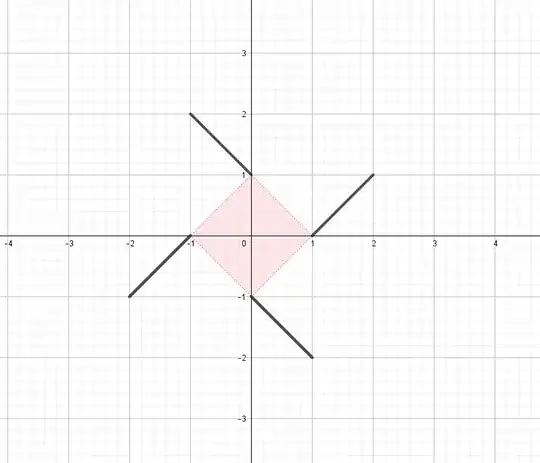
Let $S\subseteq\Bbb R$. Assume a function $f: S\to S$ has these properties:

With a $90^\circ$ counter-clockwise rotation of its graph around the origin, we get the same graph $\Gamma_f$ again. Prove that the function must be bijective.

I've seen the parametric formula: $$x'=x\cos\theta-y\sin\theta$$ $$y'=x\sin\theta+y\cos\theta$$ In my case:$$\theta=\frac{\pi}{2}$$

My first attempt was to find the properties of a function that satisfies this condition: $f(x)=y\in\Gamma_f \wedge f(-y)=x\in\Gamma_f,$ but it didn't help me. I'm not sure if I understand what "the same" means in this task.

Matcha Latte
  • 4,665
  • 4
  • 16
  • 49
  • 2
    If $f(x)=f(y)$ then the points $(x,f(x))$ and $(y,f(y))$ rotate to $(-f(x),x)$ and $(-f(y),y)$. This is the graph of a function only if $x=y$. Therefore, the function is injective. Assume $x\in S$. The point of the graph $(x,f(x))$ rotated gives $(-f(x),x)$. Since this is a point of the graph of $f$, then $f(-f(x))=x$. Therefore, all points $x\in S$ are in the image of $f$. – conditionalMethod Nov 05 '19 at 18:33
  • 1
    You can prove this by counter example. Draw a non injective function $f$. After the transformation the graph of $f$ will not be the graph of any function. So only injective functions are allowed. Now suppose you have the graph of a function $g$ inside a bounding box or some subset of $S$. If you transform the box it might be that the box is not even overlapping with the origianl box, i.e. the box must contain all of $S$. In other words $g$ must be surjective. – ty. Nov 05 '19 at 19:13

1 Answers1

0

Alert: just a long comment with the purpose of giving a visual insight

According to the post itself and what @conditionalMethod has already stated, let $r_O:\Bbb R^2\to\Bbb R^2$ be our rotation for $90^\circ$ around the origin $O(0,0)$, then: $\color{brown}{r_O:(x,f(x))\mapsto (-f(x),x))}$.

Here is a concrete example of such a function:

$$f(x)=\begin{cases}x+1,&x\in(-2,-1)\\-x+1,&x\in(-1,0)\\-x-1,&x\in(0,1)\\x+1,&x\in(1,2)\end{cases}$$ so, e.g. $$S=(-2,2)\setminus\{-1,0,1\}$$ I also high-lighted a squre with edges of length $a=\sqrt{2}$ which I found interesting. $\Gamma_f$ is black in the picture: enter image description here

Another example is the function $$\begin{cases}x=\cos\left(\alpha+k\frac\pi2\right)\\y=\sin\left(\alpha+k\frac\pi2\right)\end{cases},\quad\alpha\in\left(\arctan a,\frac\pi2\right),k\in\{1,2,3,4\},$$

whose graph consists of the four red arcs on the unit circle:

enter image description here

Matcha Latte
  • 4,665
  • 4
  • 16
  • 49