16

Since the language $L = \emptyset$ is regular, there must be a finite automaton that recognizes it. However, I'm not exactly sure how one would be constructed. I feel like the answer is trivial. Can someone help me out?

Tara B
  • 5,441
user68486
  • 161
  • 1
  • 1
  • 3

4 Answers4

14

One state, non-accepting, and no transitions. (That’s an NFA; if you want a DFA, have one transition from the state to itself for each letter of whatever alphabet is specified.)

Brian M. Scott
  • 631,399
  • 1
    Can a finite automata have no accept states at all? – user68486 Mar 25 '13 at 22:40
  • 3
    @user68486: Yes, it can: the set of acceptor states can be any subset of the set of states. – Brian M. Scott Mar 25 '13 at 22:42
  • Can you please elaborate, why the NFA can have no transitions, but the DFA must have a transition for every letter in the alphabet? – de_dust Oct 19 '17 at 09:24
  • for a moment I felt we shouldnt need any state (invisible FA :p)...seems thats not allowed... – RajS Dec 23 '17 at 15:57
  • @de_dust, it's because that one definition of DFA is that there exists a delta function $\delta: Q \times \Sigma$. It means that any state must has one transition to every symbol. – igorkf Oct 30 '21 at 03:40
7

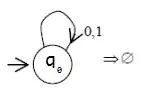
You have only one state $s$ that is initial, but not accepting with loops $s \overset{\alpha}{\rightarrow} s$ for any letter $\alpha \in \Sigma$ (with non-deterministic automaton you can even skip the loops, i.e. the transition relation would be empty).

I hope this helps ;-)

dtldarek
  • 37,969
2

Given language is "empty language".We have to construct a finite automata for this language.In general we consider "the construction of finite automata" as "the construction of DFA".So....{Let us assume input symbol as 'a' and 'b'}

(a)If we take one state(initial state) and don't show any transition of any input symbol over this state,then this structure will not be a DFA because in a DFA there should be a transition of all input symbol over each state. (b)If we take one state(initial state) and show the transition of both input symbol 'a' and 'b' over this state, then also this will not be a DFA because there should be a final state. (c)If we take one state(initial state) and show the transition of both input symbol 'a' and 'b' over this state,and making this state final also then this FA will not be acceptor of "empty language". (d)If we take one initial state 'A'(not making final it) showing the transition of both input symbol over 'A' itself AND taking one another state 'B'(as final)showing the transition of both input symbol over the "transion edge" from final state 'B' to initial state 'A'('B'is UNREACHABLE STATE here).Then this structure will be a DFA but not minimal DFA because in minimal DFA we remove UNREACHABLE STATE. (e)similarly we cannot take concept of dead state in construction of minimal DFA.

SO NOW THE EXACT SOLUTION IS :-

" TAKE ONE INITIAL STATE 'A'(not making final it) and ONE ANOTHER STATE 'B'(making it final) and SHOW transition of both input symbol 'a' and 'b' over both state A' and 'B'. BUT don't connect both states with any transition edge. This is the desired minimal DFA which accepts "empty language".

Salman Ahmad
  • 21
1

This will be the DFA

This is the DFA that iterates over (0|1)* but does not accept anything (not even empty string).

lu5er
  • 511
  • You've just said "accept empty string" and then "does not accept anything". Can you explain it better? – JB-Franco Mar 15 '17 at 22:24
  • 1
    @JB-Franco Acceptance of empty thing == not accepting anything! I think you are aware of "empty language", which means "no string", So to rephrase, "accepts empty string" == "accepts no string" == "does not accepts anything". If you still have problems, please comment. – lu5er Mar 17 '17 at 12:17
  • Thanks! - The fact you have explained in the above about DFA accepting empty string, can be related to what I have asked here: Why in a DFA the empty string distinguishes any accept state from any reject state? – JB-Franco Mar 17 '17 at 19:41
  • 1
    This answer is wrong because "accepts empty string" and "accepts no string" are not the same! The NFA with only one state and no transitions accepts no strings if the state is non-accepting, and the empty string (but no other strings) if the state is accepting. Similarly, a DFA can accept only the empty string and no others by having a start state which is accepting and then all transitions point to a non-accepting trap state like the one in this answer. – Benjamin Cosman May 29 '17 at 16:13
  • @BenjaminCosman, answer me one thing, what do you mean by empty string? – lu5er May 30 '17 at 17:25
  • A string is a finite sequence of symbols like 10010. The empty string is the sequence of zero symbols, usually written $\varepsilon$. A DFA computes on a string by reading one symbol at a time and taking the appropriate transition, so if you give it the empty string then it takes no transitions at all and accepts or rejects based on the start state. – Benjamin Cosman May 30 '17 at 17:30
  • A language is a set of strings, like {1, 000, 10010}. A DFA recognizes a language if it accepts every string in the language and rejects every other string. The empty language is the set {} (often written $\emptyset$); i.e. the set with no strings at all. It is not the same thing as the set {$\varepsilon$}, i.e. the set that contains one string that happens to be the empty string, nor is it the same thing as the empty string $\varepsilon$ itself. – Benjamin Cosman May 30 '17 at 17:32
  • @BenjaminCosman, Yes! That's correct. Now tell me, can you make a DFA that accepts an empty language AND again does not accept zero-length string? – lu5er May 30 '17 at 18:04
  • Yes: The DFA from your answer recognizes the empty language and does not accept the zero-length string. (Any DFA that does accept $\varepsilon$ would have a non-empty language.) To clarify, I'm not saying that your DFA is wrong; I'm saying that your explanation is wrong: You are correct to say that your DFA "does not accept anything", but that is in direct contradiction to your statement that it "accepts empty string", which it most certainly does not - the only DFAs that accept $\varepsilon$ are those whose start state is accepting. – Benjamin Cosman May 30 '17 at 18:24
  • My guess is that this is a language issue, because in neither standard English nor mathematical English is "accepts empty string" even quite gramatically correct, let alone means "accepts no string". I'm currently TAing an automata theory course, actually, and would be happy to have the instructional team independently evaluate this answer if you'd like. – Benjamin Cosman May 30 '17 at 18:46
  • Could you please just edit your answer to change "empty string" to "no strings"? To your mind they're equivalent and to mine you'd be fixing the answer, so everyone is happy. The alternative is that I go to my team for confirmation, which may have the side-effect of costing you a lot of rep in downvotes if I'm right. – Benjamin Cosman Jun 01 '17 at 05:52
  • @BenjaminCosman, Why won't I? But only after you give a proper explanation that IF my DFA is correct AND it accepts no strings THEN it also does not accepts zero-length strings. Well, I'm not afraid of downvotes or loss of reputations if it's constructive and we all learn something new out of it. :) – lu5er Jun 02 '17 at 12:08
  • What would you say the language of this DFA is, and do you think it is the same or different from yours? – Benjamin Cosman Jun 05 '17 at 15:19
  • @BenjaminCosman, Yes! You are absolutely correct. Made the necessary changes. :) – lu5er Jun 07 '17 at 23:18