Find a graph such that $\kappa(G) < \lambda(G) < \delta(G)$

Question

How would I go about constructing a graph that satisfies this inequality? I am new to graph theory so I'm not sure where to start. Note that:

$\kappa(G)$ is the vertex-connectivity of G, the size of the smallest separating set of G. (A separating set is a set of vertices of G whose deletion from the graph makes the graph become disconnected).

$\lambda(G)$ is the edge-connectivity of G, the size of the smallest disconnect set of G. (A disconnected set is a set of edges of G whose deletion from the graph makes the graph become disconnected).

$\delta(G)$ is the minimum degree of G (i.e. the degree of the vertex of G with the minimum degree).

Answer 1

Let $G$ be the following graph:

Then $\kappa(G)=1$ (remove its middle point), $\lambda(G)=2$ (remove $a$ and $b$) and $\delta(G)=3$.

Answer 2

Given integers $k,\ell,d$ with $1\le k\le\ell\le d$, here's how you can construct a graph $G$ with $\kappa(G)=k$, $\lambda(G)=\ell$, and $\delta(G)=d$.

Take five disjoint sets $V_1,V_2,V_3,V_4,V_5$ with $|V_1|=1$, $|V_2|=d$, $|V_3|=\ell$, $|V_4|=k$, $|V_5|=d$, and take a surjection $f:V_3\to V_4$.

The vertex set of $G$ is $V_1\cup V_2\cup V_3\cup V_4\cup V_5$.

For the edge set of $G$ take all edges $xy$ where $\{x,y\}\subseteq V_1\cup V_2$ or $\{x,y\}\subseteq V_2\cup V_3$ or $\{x,y\}\subseteq V_4\cup V_5$, and all edges $xy$ where $x\in V_3$ and $y=f(x)\in V_4$.

Note that $G$ can be disconnected by removing either the $k$ vertices in $V_4$ or the $\ell$ edges between $V_3$ and $V_4$, and that the vertex in $V_1$ has degree $d$. A little consideration will show that in fact $\kappa(G)=k$, $\lambda(G)=\ell$, and $\delta(G)=d$.

Answer 3

$\kappa(G)$ is the vertex-connectivity of G.

$\kappa'(G)$ is the edge-connectivity of G.

$\delta(G)$ is the minimum degree of G.

Reference

Answer 4

ɑ(G) is the vertex connectivity of G.

λ(G) is the edge connectivity of G.

δ(G) is the minimum degree of G.

Answer 5

watch out! mma GraphData hasn't implemented all graphs for vertex-number =8,9,10,11,12...

---

You can use Mathematica GraphData function to find the answer.

Here is an example.

func = {#, GraphData[#, "VertexConnectivity"], 
    GraphData[#, "EdgeConnectivity"], 
    GraphData[#, "MinimumVertexDegree"]} &;
selectedGraphs = 
 GraphData[All] // Map[func, #] & // 
  Select[#, (Part[#, 2] < Part[#, 3] && Part[#, 3] < Part[#, 4]) &] &

{{{"Quartic", {11, 1}}, 1, 2, 4}}   (* just find this, maybe exsits more*)
(Note that mma GraphData hasn't implemented all graphs for vertex-number =8,9,10,11,12...)

(*Plot the satisfied graphs*)
GraphicsGrid[
 Partition[GraphData /@ Map[Part[#, 1] &, selectedGraphs], UpTo[5]]]

For this graph,

• vertex-connectivity is $1$
• edge-connectivity is $2$
• minimum-vertex-degree is $4$

Answer 6

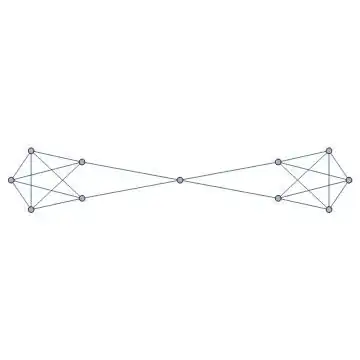
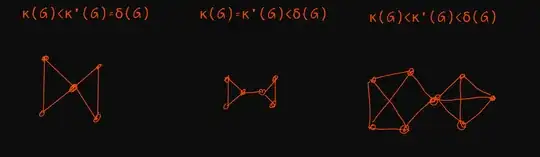Illustrated by this answer, I came up a simpler construction: begin with 3 numbers $\kappa\leq\lambda\leq\delta$, we can consider two disjoint set $V_1, V_2$, where $|V_1|=|V_2|=\delta+1$, then construct two complete graph on it respectively, i.e. $K_{\delta+1}[V_1]+K_{\delta+1}[V_2]$, which makes minimum degree is $\delta$. Then choose two subsets $X\subset V_1, Y\subset V_2$ where $|X|=\lambda\geq |Y|=\kappa$, and choose a surjection $f:X\to Y$ (those are all arbitary), join all vertices $x\in X$ to $f(x)$, that is add $\kappa$ edges $E'=\{\{x,f(x)\}|x\in X\}$. Now what we need is the graph $$G=(V_1\sqcup V_2,E), E=E(K_{\delta+1}[V_1])\sqcup E(K_{\delta+1}[V_2])\sqcup E'.$$ It's easy to show that $\kappa(G)=\kappa, \lambda(G)=\lambda, \delta(G)=\delta$: given two vertices $u\in V_1, v\in V_2$ there are at most $\kappa$ internal disjoint $uv$-path and at most $\lambda$ edge disjoint $uv$-path, and there exists a vertex whose degree is $\delta$. At last, $v(G)=2\delta+2, e(G)=\delta(\delta+1)+\kappa$, it's a better construction than 1.

Let $V_1=\{1,\cdots,\delta+1\}, V_2=\{\delta+2,\cdots,2\delta+2\}, f(i)=\delta+1+\min(i,\kappa) (1\leq i\leq \lambda)$, we can use Mathematica to visualize it:

{\[Kappa], \[Lambda], \[Delta]} = {5, 5, 5};(*Need \[Kappa]<=\[Lambda]<=\[Delta]*)
f[i_] := If[1 <= i <= \[Lambda], Min[\[Delta] + 1 + i, \[Delta] + 1 + \[Kappa]]];
bipolyCoord[n_] := Join[Table[ReIm[-E^(-2 Pi  i  I/n) - 1.5], {i, n}], Table[ReIm[E^(2 Pi  i  I/n) + 1.5], {i, n}]];
G = EdgeAdd[GraphDisjointUnion[CompleteGraph[\[Delta] + 1], CompleteGraph[\[Delta] + 1]], 
    Table[i <-> f[i], {i, \[Lambda]}], VertexCoordinates -> bipolyCoord[\[Delta] + 1], VertexLabels -> Automatic]
{VertexConnectivity, EdgeConnectivity, Min@VertexDegree[#] &}[G] // Through

where I show $V_1,V_2$ on vertices of two regular $(\delta+1)$-polygon.