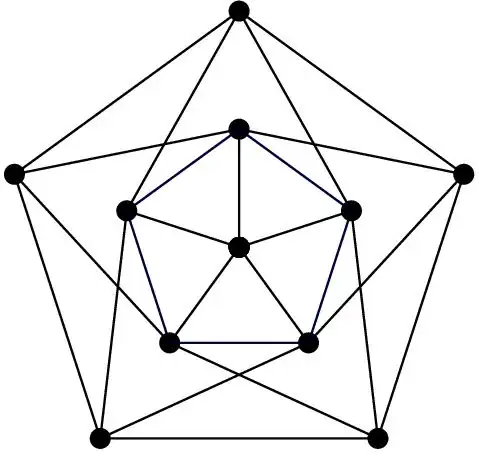
How do I prove this graph is nonplanar? It has 11 vertices and 25 edges, with a girth of 3.
Asked
Active
Viewed 1,431 times
1
Misha Lavrov
- 159,700
Viper6
- 21
-
4Possibly helpful: Kuratowski's Theorem says that a graph is nonplanar if and only if it contains either $K_5$ or $K_{3, 3}$ (or both). – Brian Tung Oct 10 '19 at 16:19
-
Your question is phrased as an isolated problem, without any further information or context. This does not match many users' quality standards, so it may attract downvotes, or be put on hold. To prevent that, please edit the question. This will help you recognise and resolve the issues. Concretely: please provide context, and include your work and thoughts on the problem. These changes can help in formulating more appropriate answers – The Demonix _ Hermit Oct 10 '19 at 16:33
-
It is not a duplication of that problem there are a different number of vertices and edges in this graph. – Viper6 Oct 10 '19 at 16:46
-
1The method in this answer solves the problem quickly. – Misha Lavrov Oct 10 '19 at 17:00
-
Thanks, but I know the graph is non-planar, I'm just not sure how to write a proof of that – Viper6 Oct 10 '19 at 17:03
-
Why can't you write a proof using the Hamilton cycle argument? – saulspatz Oct 10 '19 at 17:06
-
how does a hamilton cycle prove non planar? – Viper6 Oct 10 '19 at 17:24
-
Read the answer that Misha linked. Once you have found a Hamilton cycle in a graph, it's easy to determine whether or not it is planar. – saulspatz Oct 10 '19 at 17:26
-
I don’t think that’s a valid way to prove it though, just a way to check – Viper6 Oct 10 '19 at 17:55
-
Of course it's a valid way to prove it. This is Tutte's theorem on conflict graphs. See https://math.stackexchange.com/questions/533177/where-can-i%20-find-a-proof-of-tuttes-theorem – saulspatz Oct 10 '19 at 18:09
1 Answers
3
Delete the center vertex and you're left with a graph $G$ that has $10$ vertices and $20$ edges. By Euler's formula, if $G$ were planar, it would need to have $12$ faces in any plane embedding.
Since $G$ has no triangles (all triangles of the original graph passed through the center vertex, which you can check), each face would have at least $4$ sides. This gives at least $48$ edges, counted twice; therefore $G$ would need to have at least $24$ edges. But $G$ has only $20$ edges, contradiction.
Misha Lavrov
- 159,700
-
Also, by removing the $5$ inner edges of $G$, you get a subgraph which is a subdivision of $K_5$. – bof Oct 10 '19 at 20:47
-
@bof You're right, but I'm personally really bad at finding minors and subdivisions, so I try to find other arguments whenever that's possible. – Misha Lavrov Oct 10 '19 at 20:49